Pitagorasz-tétel

[size=150]Pitagorasz ión származású, a Kis Ázsiához közel eső Samos szigeten született (i.e.586 és 570 között különböző források szerint) Görög filozófus,Mnesarchos fia[/size] — Pitagorasz ión származású, a Kis Ázsiához közel eső Samos szigeten született (i.e.586 és 570 között különböző források szerint) Görög filozófus,Mnesarchos fia

Pitagorasz munkássága

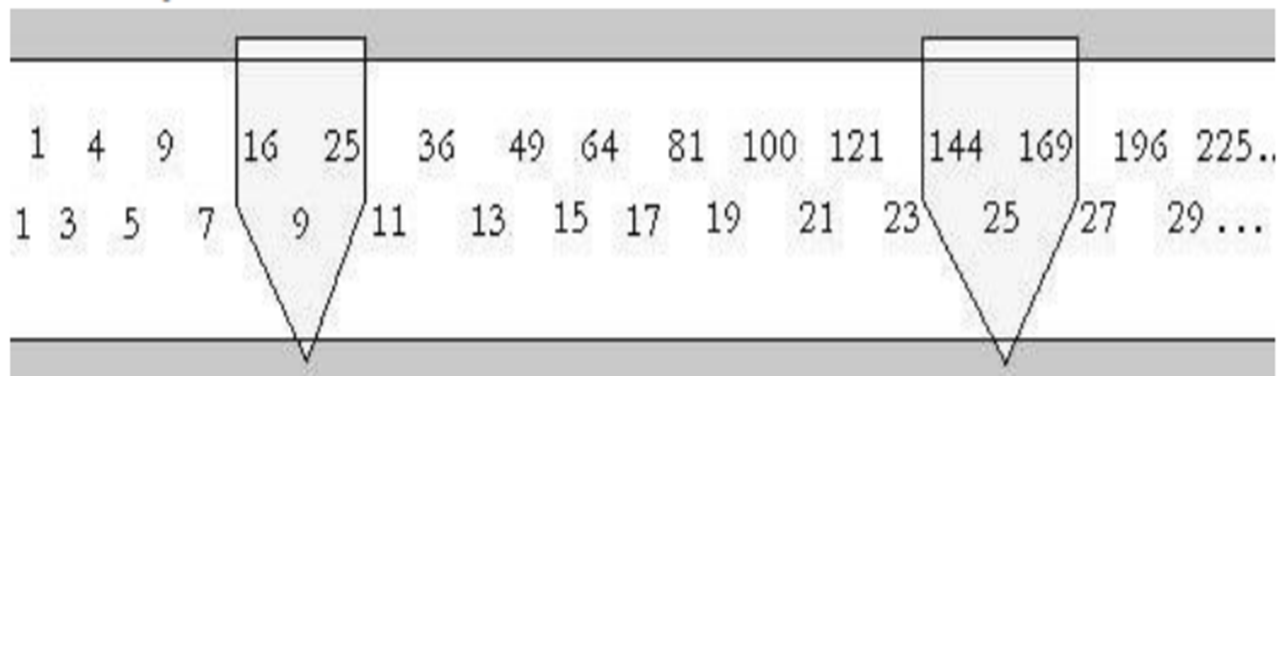
A Püthagoreus Testvériség tagjai ismerték a 4 tökéletes számot. Ők tanulmányozták először a prímszámokat is. Eljutottak az irracionális számok felfedezéséig is, de ezt titokként kezelték. Megtalálták a pitagoraszi számhármasok előállításának módját. A számtani középet és a különböző középértékeket is ők vezették be. Ismerték a szabályos testek közül a tetraédert, a kockát és a dodekaédert. Pitagorasz és tanítványai a matematikát szakterületekre osztották. (aritmetika, zene, geometria és csillagászat, azaz szám, elrendezés, forma és mozgás).

Tudományos eredményei

Bár a róla elnevezett tételt nem ő találta fel, sőt nem is ő bizonyította először, és nem tudni mi az amire valóba ő jött rá. És mi az , amire tanítványai. Személyesen fedezte fel a rezonancia alaptörvényét, miszerint a hang magassága a rezgő húr hosszának függvénye. Pitagorasz bizonyítás nélkül kimondta, hogy az egyenlő kerületű síkidomok között a kör területe a legnagyobb, és az egyenlő felületű testek között pedig a gömb térfogata a maximális.

[size=150]Az ókori egyiptomiak mindenesetre ismerték, hogy 3,4 és 5 oldalú háromszög derékszögű.
És ezt ügyesen használták földterület mérésében és a piramisok építésében.
Vettek egy hosszú kötelet, arra
egyforma közönként 3+4+5=12 csomót kötöttek, összefogták 3,4 és 5 oldalú
háromszöggé és ezzel mérték a derékszöget.[/size] — Az ókori egyiptomiak mindenesetre ismerték, hogy 3,4 és 5 oldalú háromszög derékszögű. És ezt ügyesen használták földterület mérésében és a piramisok építésében. Vettek egy hosszú kötelet, arra egyforma közönként 3+4+5=12 csomót kötöttek, összefogták 3,4 és 5 oldalú háromszöggé és ezzel mérték a derékszöget.

A tétel

Bármely derékszögű háromszög leghosszabb oldalának (átfogójának) négyzete megegyezik a másik két oldal (a befogók) négyzetösszegével. Tehát: ha egy háromszög derékszögű, akkor a leghosszabb oldalára emelt négyzet területe a másik két oldalra emelt négyzetek területének összegével egyenlő. A szokásos jelölésekkel (c az átfogó):

A Pitagorasz-tétel másik megfogalmazása:

Tetszőleges derékszögű háromszögben a befogók fölé írt négyzetek területeinek összege megegyezik az átfogó fölé írt négyzet területével.