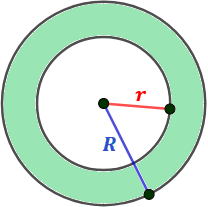
Corona Circular
- Autor:
- JLF
En esta página definimos corona circular y proporcionamos las fórmulas para calcular su área y su perímetro.
Definición
Una corona circular es la figura geométrica delimitada por dos circunferencias con el mismo centro (concéntricas) y radios distintos (R>r):
En la representación, R es el radio de la circunferencia exterior y r es el radio de la circunferencia interior.
En la representación, R es el radio de la circunferencia exterior y r es el radio de la circunferencia interior.
Fórmulas
Las fórmulas del área y del perímetro de una corona circular se obtienen a partir de las fórmulas de la circunferencia. Recordamos que el área delimitada por una circunferencia de radio R es πR^2 y su perímetro es 2πR.
Si R es el radio mayor (circunferencia exterior) y r el radio menor (circunferencia interior) de una corona circular, entonces:
El área de la corona circular es
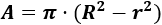El perímetro de la corona circular es
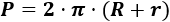
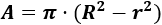El perímetro de la corona circular es
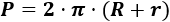
Ejemplo (Problema 1)
Calcular el área y el perímetro de una corona circular delimitada por dos circunferencias con radios 2 y 4 metros.
Solución:
El radio de la circunferencia exterior es R=4m y el radio de la circunferencia interior es r=2m. Por tanto, el área de la corona circular es
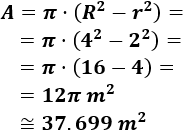Y el perímetro es
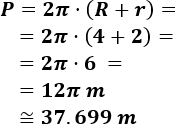
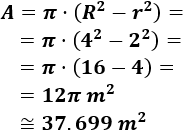Y el perímetro es
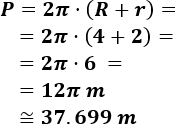
Problemas propuestos
Problema 2
Una piscina con forma circular y perímetro 30π metros tiene una isla circular con un radio de 2 metros. Calcular la superficie de agua de la piscina.
Problema 3
Explicar por qué el área de una corona circular es A=π⋅(R^2−r^2) y su perímetro es P=2⋅π⋅(R+r).
Problema 4
Escribir la ecuación de una corona circular delimitada por las circunferencias con centro en el origen y radios 1 y 3.
Problema 5
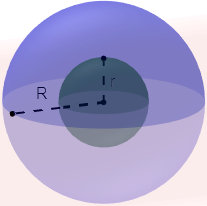Una corona esférica es la región del espacio comprendida entre dos esferas concéntricas. ¿Cuál es su volumen?
Una piscina con forma circular y perímetro 30π metros tiene una isla circular con un radio de 2 metros. Calcular la superficie de agua de la piscina.
Problema 3
Explicar por qué el área de una corona circular es A=π⋅(R^2−r^2) y su perímetro es P=2⋅π⋅(R+r).
Problema 4
Escribir la ecuación de una corona circular delimitada por las circunferencias con centro en el origen y radios 1 y 3.
Problema 5
Una corona esférica es la región del espacio comprendida entre dos esferas concéntricas. ¿Cuál es su volumen?Las soluciones a los problemas propuestos están en la página Corona circular: área, perímetro y problemas resueltos.
Recursos
- Arcos Circulares
- Sectores Circulares
- Áreas de figuras con formas circulares
- Problemas de Cuadrados
- Problemas de Pentágonos Regulares
- Problemas de Hexágonos Regulares
- Calculadoras de Pentágonos
- Calculadoras de Hexágonos
- Calculadoras de Circunferencias, arcos, sectores y coronas
- Áreas de Triángulos
- Problemas de trigonometría (seno y coseno)
- Teorema de Pitágoras
- Ejercicios interactivos de Geometría 2D
- Matesfacil.com