9 Goldener Schnitt/ Satz des Pythagoras
Aufgabe 1.1
Befolge die Euklidische Konstruktionsanleitung des Goldenen Schnitts, um diesen selbst zu erstellen und zu messen. Man kann den Goldenen Schnitt ausschließlich mit Zirkel und Lineal konstruieren. Natürlich darfst du auch alle anderen Werkzeuge von Geogebra und nicht nur die klassischen Werkzeugen von Euklid nutzen.
Die Symbole der Werkzeuge am Ende jedes Schrittes sollen dir helfen, welche Werkzeuge man klassischerweise nutzt, um das gewünschte Ergebnis zu erzielen.
1. Setze die Punkte und in beliebigem Abstand zueinander. Zeichne ein. 
2. Konstruiere den Punkt so, dass orthogonal zu steht und die Länge hat . Zeichne und ein. 
3. Konstruiere den Punkt so, dass er auf liegt und . 
4. Konstruiere den Punkt so, dass er auf liegt und . 
Die Strecken und stehen nun im Goldenen Schnitt. Das bedeutet, dass . Mithilfe des Satz des Pythagoras kannst du beweisen, dass diese Gleichung gilt (Bonusaufgabe am Ende).
5. Errechne und , indem du die beiden Brüche links in der Algebra-Funktion notierst. Diese beiden Werte sollten identisch sein. Verschiebe nun die Position von . Die beiden Werte sollten gleich bleiben, egal wie lange ist.
2. Konstruiere den Punkt so, dass orthogonal zu steht und die Länge hat . Zeichne und ein.
3. Konstruiere den Punkt so, dass er auf liegt und .
4. Konstruiere den Punkt so, dass er auf liegt und .
Die Strecken und stehen nun im Goldenen Schnitt. Das bedeutet, dass . Mithilfe des Satz des Pythagoras kannst du beweisen, dass diese Gleichung gilt (Bonusaufgabe am Ende).
5. Errechne und , indem du die beiden Brüche links in der Algebra-Funktion notierst. Diese beiden Werte sollten identisch sein. Verschiebe nun die Position von . Die beiden Werte sollten gleich bleiben, egal wie lange ist.Aufgabe 1.2
Wie lautet das Ergebnis von ? Du sollst das Ergebnis als Dezimalzahl mit zwei Stellen nach dem Komma angeben.
Aufgabe 1.3
Berechne das Verhältnis . Dieses wirst du in der nächsten Aufgabe brauchen. Gib dein Ergebnis an, auch hier mit zwei Nachkommastellen.
Aufgabe 2.1
Hier siehst du ein Bild vom Karlsruher Schloss sowie ein Maßband, das entsprechend des Goldenen Schnitts eingefärbt ist. Verschiebe das Maßband und finde heraus, wo im Karlsruher Schloss der Goldene Schnitt als Verhältnis gewählt wurde!
Aufgabe 2.2
Wo konntest du zwischen den unten genannten Strecken einen markanten Punkt im Goldenen Schnitt finden?
Aufgabe 2.3
Erstelle nun dein eigenes Goldener-Schnitt-Maßband und füge dein eigenes Bild ein. Folge dazu folgender Konstruktionsbeschreibung:
1. Setze die Punkte und an beliebigen Stellen. Weise außerdem einer Variablen die Zahl zu, die du oben errechnet hast (, ). 
2. Konstruiere nun den Punkt , der im Verhältnis von zwischen und liegt. Definiere in der Algebra-Funktion mithilfe seiner - und -Koordinate in Abhängigkeit derer der anderen beiden Punkte:
mit und .
Wenn du jetzt oder verschiebst, sollte sich dynamisch mitbewegen und im gewählten Verhältnis zwischen und bleiben.
Nach diesem Schritt kannst du auch die Koordinatenachsen ausblenden, falls du dies noch nicht getan hast. Diese waren dazu da, damit man die Koordinatenzuweisung von besser nachvollziehen kannst.
3. Konstruiere die Strecken und und färbe sie in den Einstellungen verschiedenen Farben (Rechtsklick auf Objekt). Wenn du magst, kannst du die Endpunkte der Strecken in der entsprechend selben Farbe einfärben.
4. Ziehe durch eine orthogonale Strecke, deren Endpunkte jeweils etwa von entfernt sind. Färbe auch diese Strecke ein.
5. Über die Einstellungen kannst du nun alle Beschriftungen und Hilfspunkte verbergen, sodass das Maßband am Ende aussieht wie bei Aufgabe 2.1.
6. Füge nun ein Bild ein, das du auf dem Hausaufgabenblatt heruntergeladen hast. Wähle dazu "Bild einfügen". Das Bild kannst du mit den zwei automatisch erstellten Punkten in der Größe und Position verschieben. Die Punkte kannst du ausblenden, sobald das Bild an der gewünschten Position ist. Über die Grundeinstellungen kannst du das Bild fixieren, sodass du es nicht aus Versehen verschiebst. Außerdem kann man das Bild dort zu einem Hintergrundbild machen, damit es nicht dein Maßband verdeckst. 
Nun solltest du dein eigenes Bild auf den Goldenen Schnitt prüfen können. Viel Spaß beim Suchen!
2. Konstruiere nun den Punkt , der im Verhältnis von zwischen und liegt. Definiere in der Algebra-Funktion mithilfe seiner - und -Koordinate in Abhängigkeit derer der anderen beiden Punkte:
mit und .
Wenn du jetzt oder verschiebst, sollte sich dynamisch mitbewegen und im gewählten Verhältnis zwischen und bleiben.
Nach diesem Schritt kannst du auch die Koordinatenachsen ausblenden, falls du dies noch nicht getan hast. Diese waren dazu da, damit man die Koordinatenzuweisung von besser nachvollziehen kannst.
3. Konstruiere die Strecken und und färbe sie in den Einstellungen verschiedenen Farben (Rechtsklick auf Objekt). Wenn du magst, kannst du die Endpunkte der Strecken in der entsprechend selben Farbe einfärben.
4. Ziehe durch eine orthogonale Strecke, deren Endpunkte jeweils etwa von entfernt sind. Färbe auch diese Strecke ein.
5. Über die Einstellungen kannst du nun alle Beschriftungen und Hilfspunkte verbergen, sodass das Maßband am Ende aussieht wie bei Aufgabe 2.1.
6. Füge nun ein Bild ein, das du auf dem Hausaufgabenblatt heruntergeladen hast. Wähle dazu "Bild einfügen". Das Bild kannst du mit den zwei automatisch erstellten Punkten in der Größe und Position verschieben. Die Punkte kannst du ausblenden, sobald das Bild an der gewünschten Position ist. Über die Grundeinstellungen kannst du das Bild fixieren, sodass du es nicht aus Versehen verschiebst. Außerdem kann man das Bild dort zu einem Hintergrundbild machen, damit es nicht dein Maßband verdeckst.
Nun solltest du dein eigenes Bild auf den Goldenen Schnitt prüfen können. Viel Spaß beim Suchen!Aufgabe 3
In dieser Aufgabe wird nun mithilfe der Fibonacci-Zahlen eine Fibonacci-Spirale erstellt. Dazu werden nacheinander Quadrate mit den Seitenlängen der Fibonacci-Zahlen nebeneinander platziert und anschließend durch die gemeinsamen Eckpunkte der Quadrate die Spirale gezogen. Gehe dazu folgendermaßen vor:
1. Erzeuge die Quadrate mit den Seitenlängen , gerne auch direkt ein paar mehr. Dazu verwendest du am effizientesten vermutlich den Befehl "Regelmäßiges Vieleck". Hier gibst du nacheinander zwei Eckpunkte (deren Streck ist die Grundseite des Vielecks) und die Anzahl der Ecken an (bei uns also immer 4).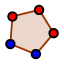 
2. Zeichne nun in die Quadrate jeweils einen Kreisbogen, indem du den Befehl "Kreisbogen" verwendest. Hier musst du nacheinander den Mittelpunkt des Kreises, dann den Start- und zuletzt des Endpunkt des Kreisbogens auswählen. Diese drei Punkte müssen immer drei Eckpunkte eines Quadrats sein und des Endpunkt in der Ecke eines Quadrats soll automatisch der Startpunkt in der Ecke des nächstgrößeren Quadrats sein. 
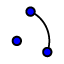3. Nun sollte die Fibonacci-Spirale bereits erkennbar sein. Blende zur Übersichtlichkeit alle Punkte und Beschriftungen der Kreissegmente aus. Achtung: Ausblenden Löschen. 
, jedoch NICHT 
.
4. Du kannst nun wieder ein Bild suchen und in das Applet einfügen, welches deine Fibonacci-Spirale beinhaltet. Ziehe es mit den beiden Eckpunkten in die richtige Größe und Position. In den Grundeinstellungen kannst du das Bild auch zu einem Hintergrundbild machen.
5. Blende nun das Bild aus (oder lösche es). Wiederhole danach die Schritte 1 und 2 (und nach Belieben 3), bis sich die Spirale mindestens zwei Mal um sich selbst gewunden hat. Durch Zoomen kannst du nun die Selbstähnlichkeit der Fibonacci-Spirale erahnen. 
Diese kommt daher, dass der Quotient zweier aufeinanderfolgenden Fibonacci-Zahlen gegen den Goldenen Schnitt konvergiert.
Informelle Begründung:
Drei aufeinanderfolgende Folgenglieder der Fibonacci-Folge , und bilden die beiden Quotienten und . Diese beiden Quotienten nähern sind gleich, wenn und exakt im Verhältnis des Goldenen Schnitts stehen.
2. Zeichne nun in die Quadrate jeweils einen Kreisbogen, indem du den Befehl "Kreisbogen" verwendest. Hier musst du nacheinander den Mittelpunkt des Kreises, dann den Start- und zuletzt des Endpunkt des Kreisbogens auswählen. Diese drei Punkte müssen immer drei Eckpunkte eines Quadrats sein und des Endpunkt in der Ecke eines Quadrats soll automatisch der Startpunkt in der Ecke des nächstgrößeren Quadrats sein.
3. Nun sollte die Fibonacci-Spirale bereits erkennbar sein. Blende zur Übersichtlichkeit alle Punkte und Beschriftungen der Kreissegmente aus. Achtung: Ausblenden Löschen. , jedoch NICHT .
4. Du kannst nun wieder ein Bild suchen und in das Applet einfügen, welches deine Fibonacci-Spirale beinhaltet. Ziehe es mit den beiden Eckpunkten in die richtige Größe und Position. In den Grundeinstellungen kannst du das Bild auch zu einem Hintergrundbild machen.
5. Blende nun das Bild aus (oder lösche es). Wiederhole danach die Schritte 1 und 2 (und nach Belieben 3), bis sich die Spirale mindestens zwei Mal um sich selbst gewunden hat. Durch Zoomen kannst du nun die Selbstähnlichkeit der Fibonacci-Spirale erahnen.
Diese kommt daher, dass der Quotient zweier aufeinanderfolgenden Fibonacci-Zahlen gegen den Goldenen Schnitt konvergiert.
Informelle Begründung:
Drei aufeinanderfolgende Folgenglieder der Fibonacci-Folge , und bilden die beiden Quotienten und . Diese beiden Quotienten nähern sind gleich, wenn und exakt im Verhältnis des Goldenen Schnitts stehen.Bonusaufgabe 4
Falls du noch Zeit hast, betrachte einige Beweise des Satz des Pythagoras in Geogebra. Diese Sammlung stammt von Land Baden-Württemberg und enthält über 100 Beweise des Satz des Pythagoras, von Euklid über Da Vinci bis hin zu einem US-Präsidenten. Der Link führt dich zu dem Beweis von Einstein, den du bereits im Vortrag kennengelernt hast.
https://www.schule-bw.de/faecher-und-schularten/mathematisch-naturwissenschaftliche-faecher/mathematik/unterrichtsmaterialien/sekundarstufe1/geometrie/pyth/beweise/einstein.html