Angoli tra due rette parallele ed una obliqua

Autor:Ilic Ferretti

LA NOMENCLATURA DEGLI ANGOLI TRA RETTE PARALLELE Una proprietà molto importante che si ha ogni volta che si considerano delle rette parallele è la relazione tra gli angoli che esse formano con una qualsiasi retta obliqua che le taglia. Nella figura sotto si vede che si formano due gruppi di quattro angoli (un gruppo per ogni retta parallela). Nel disegno i quattro angoli formati con la retta più in alto sono chiamati

(sono le lettere alfa, beta, gamma e delta minuscole dell'alfabeto greco). Gli angoli formati con la retta più in basso sono chiamati

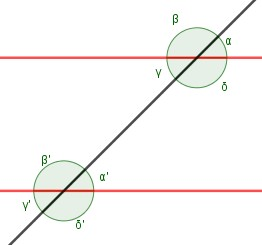
Due rette parallele tagliate da una trasversale e gli angoli che esse formano.

Dato che abbiamo otto angoli in tutto, si possono considerare molte coppie di angoli diversi, ognuna delle quali gode di una certa proprietà: è quindi necessario DARE DEI NOMI A QUESTE COPPIE DI ANGOLI in modo da non fare confusione. GLI ANGOLI CORRISPONDENTI Le coppie di angoli a cui abbiamo dato nomi simili, cioè quelli che sono formati dalle semirette corrispondenti in alto ed in basso, sono detto appunto corrispondenti. Ad esempio

sono due angoli corrispondenti, così come

, etc... ALTRE COPPIE DI ANGOLI Vengono definiti altri nomi per altre coppie di angoli, in particolare due angoli si dicono:

interni se sono interni alla fascia definita dalle due rette parallele, esterni se sono posizionati esterni ad essa.
alterni se uno è dalla parte opposta dell'altro rispetto alla retta obliqua, coniugati se sono dalla stessa parte rispetto alla retta obliqua.

Avremo quindi che ad esempio gli angoli

sono alterni esterni, perchè sono da due parti opposte rispetto alle rette oblique (alterni) e sono all'esterno della fascia delle rette parallele. L'altra coppia di angoli alterni esterni è formata dagli angoli

. Gli angoli

sono invece coniugati (dalla stessa parte rispetto alla retta obliqua) interni (all'interno della fascia). E così via. Cerca di individuare le varie coppie di angoli nella figura sotto. Muovendo gli interruttori puoi ricreare tutte le combinazioni e verificare le tue ipotesi.

LE RELAZIONI TRA LE COPPIE DI ANGOLI Le coppie di angoli individuate dalla nomenclatura che abbiamo definito stanno sempre in certe relazioni particolari, che permettono di dedurre proprietà interessanti delle figure che li contengono. NOTA: per "coppia" intendiamo due angoli adiacenti ognuno ad una diversa delle due rette parallele (uno "in alto" ed uno "in basso", o se preferisci uno con il simbolo di ' ed uno senza.). Questo perché le relazioni tra gli angoli nello stesso incrocio (ad esempio

) sono già note (sono opposti oppure adiacenti) e non interessanti rispetto al fatto di avere due rette parallele. La proprietà fondamentale è questa: due angoli alterni (non importa se interni o esterni) sono sempre congruenti tra loro. Ad esempio

(alterni interni) Da questa derivano le altre relazioni, che puoi dimostrare facilmente da sola/o sfruttando gli angoli opposti al vertice ed adiacenti:

due angoli coniugati sono sempre supplementari tra loro. Ad esempio e sono supplementari
due angoli corrispondenti sono sempre congruenti tra loro. Ad esempio

IL QUINTO POSTULATO DI EUCLIDE E LE GEOMETRIE NON EUCLIDEE La proprietà fondamentale che abbiamo enunciato non può essere dimostrata, perché in realtà si tratta di un assioma, o postulato, cioè di un dato di partenza che assumiamo essere vero perché corrisponde a quello che percepiamo nella realtà. Infatti questa relazione (o per essere più precisi la relazione 1. che come tu stessa/o hai dimostrato è strettamente collegata ad essa) è equivalente a dire che due rette parallele non si incontrano in nessun punto. Questa affermazione ci sembra naturale ed indiscutibile, ma in realtà non siamo in grado di escludere che due rette parallele non si incontrino in un qualche punto infinitamente lontano, proprio perché per definizione non possiamo verificare cosa succede "infinitamente lontano". È possibile fare scelte diverse da questo postulato, noto come quinto postulato di Euclide, e costruire delle geometrie dette "non euclidee", chiamate così perché alternative a quella costruita dall'antico studioso greco, che si attenne alla geometria corrispondente al suo postulato ed alla percezione comune della realtà - percezione limitata al contesto in cui viviamo, cioè un contesto finito e piuttosto limitato: come abbiamo detto non siamo in grado di verificare cosa succede "infinitamente lontano" (e se le rette lì si incontrano o no), semplicemente perché non ci siamo mai stati. Non a caso le geometrie non euclidee hanno un'applicazione pratica nel cercare di capire su quali leggi geometriche sia strutturato l'universo - lui sì che si occupa di dimensioni "infinitamente lontane"!

Angoli tra due rette parallele ed una obliqua

Nuevos recursos

Descubrir recursos

Descubre temas