Begriffe und Vereinbarungen
Alles ist relativ?
Der Effekt ist vielen bekannt: Man schaut im Bahnhof aus dem Zugfenster auf einen anderen Zug und ist unsicher, welcher von beiden sich bewegt. Erst ein ein Blick auf den Rest der Welt löst das Gefühl auf.
Ohne diesen Blick nach außen ist die Lage aber hoffnungslos: Es gibt keine keine Möglichkeit, die gleichförmige Bewegung des Zuges innerhalb des Zuges nachzuweisen, ohne äußere Referenzen zu verwenden.
Das bedeutet aber zwangsläufig: Ruhe und gleichförmige Bewegung sind nicht unterscheidbar und damit gleichberechtigte Zustände. Eine absolute Bewegung gibt es nicht, ein Koordinatensystem ist so gut wie irgendein anderes - solange keine Beschleunigungen auftreten. Dieser Umstand wird als Galileisches Relativitätsprinzip bezeichnet.
Wenn aber alle Koordinatensysteme gleichberechtigt sind - wie lassen sich Beobachtungen (und das heißt vor allem: Experimente, Messdaten und physikalische Theorien) in verschiedenen Systemen vergleichen? Die Kernfrage lautet daher: Wie sieht ein Experiment aus einem anderen System betrachtet aus? Offenbar
benötigt man dazu Formeln zur Umrechung zwischen den Systemen. Solche Transformationen sind
Gegenstand der Relativitätstheorie(n).
Koordinatensysteme
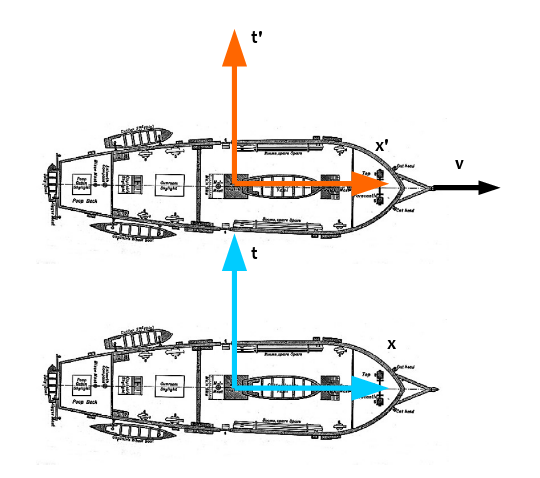
Für die Untersuchungen werden zwei Koordinatensysteme auf Schiffen betrachtet. Auf spiegelglatter See ist nicht zu erkennen, ob sich nur eines oder beide bewegen. Da es aber ohnehin keine Rolle spielt, kann man ohne Beschränkung der Allgemeinheit das untere, blaue Schiff als ruhend betrachten. Zur Vereinfachung gelten ab jetzt folgende Festlegungen:
- Anders als bisher üblich wird die x-Achse waagerecht und die t-Achse senkrecht gezeichnet.
- Man legt die x-Achsen der Systeme parallel und in Bewegungsrichtung des oberen Schiffes.
- Die Koordinaten im O-System (wie 'orange' oder 'oben') werden mit einem Strich versehen, um sie von den Koordinaten des B-Systems (blau) zu unterscheiden.
- Zum Zeitpunkt
t=0liegen beide Nullpunkte auf derselben Höhe:x'(0)=x(0)=0.