Graphen gebrochen-rationaler Funktionen
Graphen gebrochen-rationaler Funktionen
Du hast schon Graphen gebrochen-rationaler Funktionen gesehen. Klaus dagegen anscheinend nicht. Er
hat die Funktionsvorschrift gegeben und dazu eine Wertetabelle erstellt:

Mithilfe derer zeichnet er folgenden Graphen:
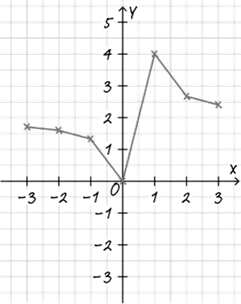
Aufgabe: a) Sieh dir den Funktionsterm noch einmal an und bestimme die Definitionslücke. Dieser Lücke wird kein Funktionswert zugeordnet! Definitionslücke: x =
Taucht sie in Klaus‘ Wertetabelle auf?
a) Plotte nun selbst die Funktion und beschreibe kurz in deinem Übungsheft den Verlauf der Funktion links und rechts von der Definitionslücke. Nutze dazu die Zoom-Funktion des Plotters.
Benenne den Fehler, den Klaus gemacht hat.
Hinweis: Klicke "Antworten überprüfen", um einen Hinweis zu erhalten.

Und weiter geht es mit dem Hefteintrag:
Graph:
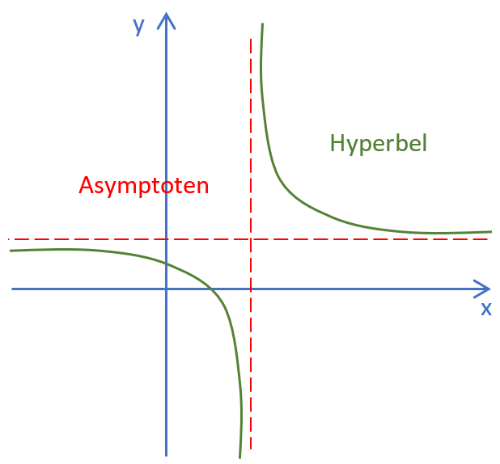
Bei Definitionslücken haben die Graphen gebrochen-rationaler Funktionen so genannte senkrechte Asymptoten. Das sind Geraden, denen sich der Graph beliebig anschmiegt, ohne sie zu berühren.
Aufgabe: Betrachte noch einmal den eben geplotteten Graphen. Siehst du auch noch eine waagrechte Asymptote? Hinweis: Klicke "Antworten überprüfen", um einen Hinweis zu erhalten.
Gleichung der waagrechten Asymptote: y =
Aufgabe:
a) Setze nun sehr große Werte (1000, 10.000, 100.000) und sehr kleine Werte (-1000, -10.000,
-100.000) in die Funktionsgleichung von oben, , ein, und berechne die Funktionswerte.
Notiere dir die Ergebnisse auch in deinem Übungsheft und beschreibe dort (gerne auch stichpunktartig, aber nachvollziehbar) deine Beobachtungen.
b) Stelle eine Hypothese auf, woran du am Funktionsterm die waagrechte Asymptote erkennen kannst, und schreibe diese ebenfalls in dein Heft.
Überprüfe deine Hypothese, indem du in die folgenden drei Funktionsgleichungen ebenfalls die Werte +/-1000, +/- 10.000 und +/- 100.000 einsetzt und einen Bezug zu den Termen herstellst:
, und
Gleichungen der waagrechten Asymptoten der Funktionen a, b und c:
Woran erkennt man schon am Term die Gleichung der waagrechten Asymptote?


Der letzte Teil des Hefteintrags in diesem Abschnitt:
Merke: Den Graphen einer gebrochen-rationalen Funktion nennt man Hyperbel. Er besteht aus zwei nicht
verbundenen Ästen, die punktsymmetrisch zum Schnittpunkt der Asymptoten des Graphen sind.
Skizze: (bitte auch ins Schulheft übernehmen!)