Sistemas de Inecuaciones lineal
Una inecuación es una desigualdad entre dos expresiones algebraicas de una o varias incógnitas, que solo se verifica para ciertos valores de esas incógnitas; se expresa con los signos >, <, ≥ y ≤.
Ejemplo: 3x - y ≤ 8 es una inecuación.
Recordemos que las desigualdades son:
• ≥ : Mayor o igual
• > : Mayor estrictamente
• ≤ : Menor o igual
• < : Menor estrictamente
Pues bien, la diferencia más esencial entre ecuaciones e inecuaciones, es que mientras que las ecuaciones calculan puntos como hemos dicho antes, las inecuaciones calculan semiplanos (o lo que es lo mismo, trozos de plano).
Por ejemplo, recordando que estamos hablando de inecuaciones en un plano, si tenemos como resultado x<0, lo tenemos que interpretar como todos los puntos (x,y) del plano cuya x sea negativa. Si nos fijamos, todos esos puntos juntos formarían el semiplano izquierdo, es decir, el trozo de plano completo que queda a la izquierda del eje y. (Ver figura 1).
En resumen, se puede decir que la solución de un sistema de inecuaciones es la intersección de las regiones que corresponden a la solución de cada inecuación. Un sistema de inecuaciones se dice que es lineal, si en ambos lados de cada inecuación aparece una expresión de primer grado.
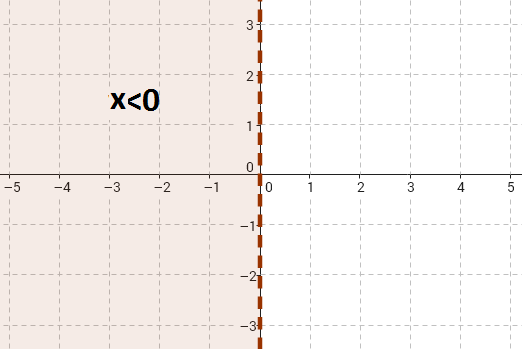
En la siguiente actividad puedes elegir si ver la ecuación asociada, toda la inecuación, o el sistema formado.
Es útil para ver cómo se va recortando la región solución al incluir cada inecuación.
Resolver una inecuación lineal
Solución gráfica de un sistema de inecuaciones lineal
Autoevaluación
¿Qué es una inecuación?
¿Cuál es la solución de un sistema de inecuaciones?
Despues de analizar las informaciones anteriores, ¿cuál es la diferencia entre un ecuación y una inecuación?
Si tenemos como resultado y>0, lo tenemos que interpretar como todos los puntos (x,y) del plano cuya y sea:
Si tenemos la inecuación x≤ 8. Esto quiere decir que x puede ser:
