ES 4.3
Given a circle, but not given its center, construct an inscribed equilateral triangle in as few steps as possible (par = 7).
PROCEDURA.
Sia c la circonferenza di base.
- Scelgo C su c e traccio la circonferenza d di centro C e raggio qualsiasi. {1 STEP}
- Sia D l'intersezione di d con c, traccio la circonferenza d di centro D e raggio uguale a prima, e. {1 STEP}
- Sia E l'intersezione delle circonferenze e, d. Traccio la retta DE che interseca c in G. {1 STEP}
- Traccio la circonferenza di centro C e raggio CG: interseca c in H. C, H, G sono i vertici del triangolo cercato. {4 STEP}
TOT. STEP: 7
DIMOSTRAZIONE.
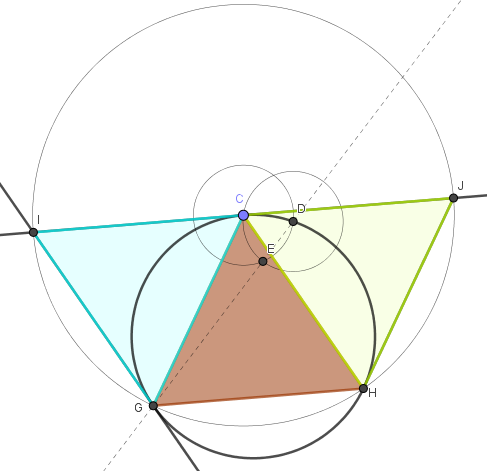
Faccio riferimento alla figura in basso.
- CI, CG, CH, CJ sono tutti congruenti perchè raggi della stessa circonferenza. Generano quindi i triangoli isosceli CIG, CGH, CHJ che hanno quindi angoli alla base congruenti.
- Osserviamo che gli angoli CGI e CHG sottendono lo stesso arco di circonferenza, pertanto sono congruenti, quindi gli angoli alla base dei triangoli CIG e CGH sono congruenti. Chiamiamo alfa l'angolo alla base dei suddetti triangoli.
- Osserviamo che gli angoli CGH e CHJ sottendono lo stesso arco di circonferenza, quindi anche gli angoli alla base del triangolo CJH saranno pari a alfa.
- Per differenza allora gli angoli ICG, GCH, HCJ saranno congruenti, ma la loro somma è 180° quindi ognuno di essi vale 60°.
- Gli angoli alla base del triangolo CGH sono congruenti e la loro somma, per differenza, è 120°. Quindi ognuno di essi misura 60°.
- Il triangolo CGH è pertanto equilatero