Definición de parámetros

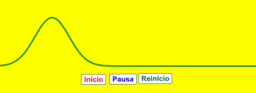
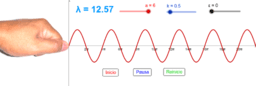
Cualquier deformación efectuada al extremo de una cuerda o un resorte elástico, largo y estirado, se transmite en toda su longitud con cierta velocidad V . Viaja un pulso ondulatorio (cresta o valle). Podemos determinar la velocidad del pulso, midiendo la distancia recorrida x y el tiempo t que tarda en recorrerla, esto es V = x / t . Claro está, estamos suponiendo que el pulso se mueve con un movimiento uniforme a lo largo de la cuerda. El applet 1 representa gráficamente un pulso propagándose a lo largo de una cuerda. Se pueden generar también pulsaciones repetidas, perturbando consecutivamente la cuerda a intervalos de tiempos iguales. Al conectar al extremo de la cuerda un dispositivo mecánico que oscile con movimiento armónico simple, se puede generar un tren periódico de pulsos, por encima (crestas) y debajo (valles) de su posición de equilibrio; es decir, resulta una onda armónica. El applet 2 representa gráficamente una onda armónica propagándose a lo largo de una cuerda. Observemos ahora esta onda propagándose en la cuerda. Las pulsaciones producidas por el generador de ondas se mueven a lo largo de ella. Si fijamos nuestra atención en un punto de la cuerda, observaremos que las pulsaciones (crestas y valles) pasan por este punto cada cierto tiempo y con cierta regularidad. El tiempo que tarda un par de pulsos consecutivos iguales, dos crestas por ejemplo, en pasar por el mismo punto, es el período T de la onda; y el número de crestas (o valles) que pasan por ese punto, por unidad de tiempo es su frecuencia f (f = 1/T). Además, a medida que la onda se mueve, la distancia entre dos pulsos iguales (dos crestas, por ejemplo) y consecutivos permanece constante. Esta distancia mínima, la cual se repite en toda la extensión de la cuerda, se denomina longitud de onda λ. En función de λ y f, la velocidad V de la onda es V = λ f. . Como se sabe, la periodicidad temporal es característica de un sistema que vibre con un movimiento armónico simple. De igual manera, la periodicidad temporal es una característica del movimiento ondulatorio y viene determinada por su período T; pero, existe otra periodicidad, la espacial, determinada por la longitud de onda λ . Más adelante precisaremos estas definiciones.La ecuación anterior obtenida para ondas mecánicas, es válida también para cualquier tipo de movimiento ondulatorio, independientemente de su naturaleza y propiedades. En conclusión tenemos que: a) Para generar una onda mecánica se requiere de un generador de onda y un medio elástico en equilibrio. b) Una onda mecánica es el producto de una serie de perturbaciones efectuada a un medio elástico en equilibrio. c) Ni el medio como un todo, ni una porción del mismo, se desplazan con las perturbaciones. d) Si el generador perturba periódicamente al medio, se generan ondas armónicas. e) La frecuencia de las ondas periódicas coincide con la frecuencia del generador. f) La periodicidad espacio temporal, es la característica fundamental del movimiento ondulatorio. La relación entre la longitud de onda λ y la frecuencia f, se expresa mediante la ecuación: V = λ f .