Conceito inicial
Conceito
Fração significa a parte de um todo e é utilizada para representar numericamente esta parte. Ainda, pode-se afirmar que fração é a razão entre dois números, obedecendo a seguinte ordem: .
As frações fazem parte do nosso cotidiano: ao realizar medições, ao comparar quantidades, em dados de pesquisas, ao dividir um lanche entre amigos, entre outros. Alguns destes exemplos, podem ser visualizados nas imagens abaixo.
Exemplos:

![Diversas frações representando quantidades/medidas.
[b]Fonte: [/b]Avon](https://www.geogebra.org/resource/mxyyd6g3/yQ9Rw790z251D94P/material-mxyyd6g3.png)
![Comparação de valores (frações equivalentes).
[b]Fonte: [/b]Avon](https://www.geogebra.org/resource/k6hcavtc/V7EVrf6D37lSUake/material-k6hcavtc.png)
Exemplo Prático
Você, ao pedir uma pizza, deseja que ela seja redonda e apresente recheios divididos igualmente sob a massa da pizza. Observe abaixo, uma imagem da massa.
![[b]Fonte: [/b]Pinterest](https://www.geogebra.org/resource/whbwsbqt/SF7IYIR4qSYSsaKD/material-whbwsbqt.png)
Como é possível fazer esta divisão dos recheios?
Como a circunferência possui um ânguo de , e queremos recheios igualmente dispostos na pizza, é necessário efetuarmos a seguinte divisão: , resultando em . Portanto, cada recheio vai ocupar um arco de na pizza.
Abaixo uma imagem, de uma das possibilidades:
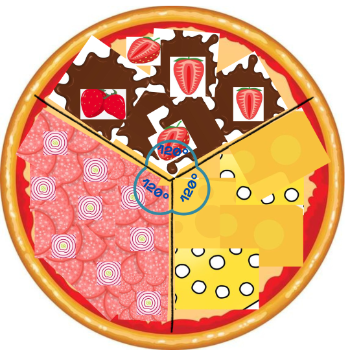
A partir da imagem acima, pode-se afirmar que o recheio de chocolate com morango representa do total de recheios presentes na pizza. O mesmo vale para os recheios de queijos e de calabresa acebolada: cada um destes recheios representa da quantidade total de reheios. Isso se deve pelo fato de a pizza ter sido comprada com recheios.
Agora, você precisa dividir cada um dos recheios, de forma igualitária, entre você e seus dois amigos. Como é possível fazer esta divisão?
Bom, cada recheio terá que ter fatias: para você e para cada um dos seus amigos. Desta maneira, como temos recheios e cada um deste vai ser composto por fatias, vamos, no final, acabar ficando com pedaços de pizza. Agora, que sabemos a quantidae, só falta descobrirmos o tamanho de cada uma destas fatias. Para isso, é necessário dividirmos os que corresponde ao tamanho de cada um dos recheios por (quantidade de fatias por recheio): . Portanto, cada fatia vai corresponder a um arco de - veja abaixo a representação desta divisão na pizza.
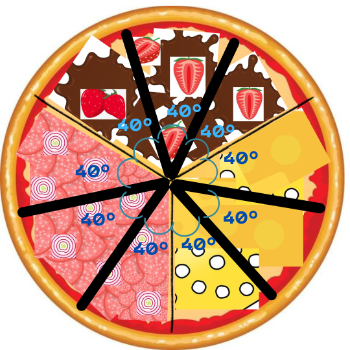
Neste estágio, temos pizza dividida em recheios e estes dividos em fatias iguais; ou seja, temos 9 pedaços de pizza (). Ainda, agora podemos afirmar que cada recheio corresponde a fatias do total de pedaços da pizza, em fração temos: , realizando a siplificação (divisão) por , obtemos - a mesma fração que havíamos encontrado no passo da distribuição dos recheios na massa da pizza.
Neste momento, também é possível delimitar a quantidade total que cada amigo vai comer da pizza em questão: pedaço de cada recheio, e como temos sabores, cada cidadão irá saborear pedaços (). Com isso, é possível afirmar que cada amigo vai comer da pizza - realizando a siplificação (divisão) por 3, obtemos - novamente a mesma relação.
Nomenclatura
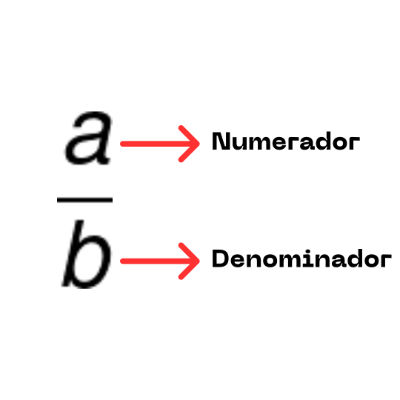
Apartir do exemplo da pizza, pode-se perceber que, dentro da estrutura geral de uma fração , o número de baixo, ou seja, o "" corresponde a quantidade total de partes em que o inteiro foi dividido. Já o elemento "" diz respeito a uma determinada parte deste inteiro. Desta maneira, estes valores recebem uma nomenclatura genérica, como pode ser observado na imagem abaixo.
Agora que sabemos a nomenclatura geral, fica mais fácil entendermos os nomes específicos de cada uma das frações. Mas, para isso é importante lembrar, que a nomenclatura vai depender do denominador (dar nome). Com isso, vamos dividir o estudo do nome das frações em dois grupos:
1° Onde o denominador é igual a , , , , , , , , , , ou .
A partir da imagem abaixo, percebe-se que neste grupo, o nome das frações vai seguir a seguinte regra:
Nome do número designação dependendo do valor do denominador.

2° Quando o denominador é formado por um número que não se enquadra no 1° grupo. Neste caso, a nomenclatura vai seguir a seguinte lei: Nome do número presente no numerador, nome do valor presente no denominador mais a palavra avos. Abaixo, segue uma imagem com alguns exemplos de frações presentes neste segundo conjunto.

Exercício 1
Qual a alternativa que apresenta corretamente a nomenclatura das frações a seguir: , , e ?
Exercício 2
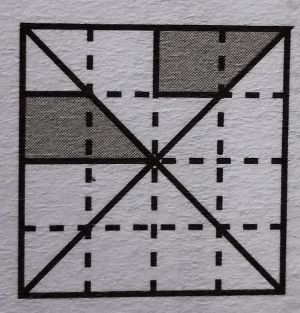
(OBMEP, 2019, ADAPTADO) Na figura acima, todos os quadradinhos do tabuleiro são iguais. Qual a fração (parte) que a região pintada cobre do quadrado maior?
Exercício 3
Escreva por extenso o nome da seguinte fração: