Übungsstunde
3D - Koordinatensystem
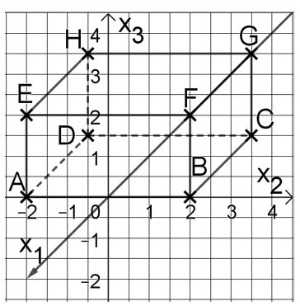
a)
Gib die Koordinaten der restlichen Eckpunkte an.
b)
Bestimme das Volumen des Quaders.
c)
Beschreibe die Lage des Quaders mit Hilfe der Oktanten.
d)
Gib die Schnittpunkte mit den Koordinatenachsen an, falls vorhanden.
e)
Gib an, in welchen Oktanten sich der Quader befindet, wenn er an der z-Achse bzw. an der xy-Ebene gespiegelt wird.
Rechnen mit Vektoren 1
a)
Bestimme die Vektoren und .
b)
Berechne die Länge der beiden Vektoren.
c)
Vergleiche die beiden Vektoren. Was fällt dir auf?
d)
Gib von beiden Vektoren den Einheitsvektor an.
e)
Berechne möglichst einfach:
Rechnen mit Vektoren 2
a)
Vereinfache: 1) -- 2) 2+--+
b)
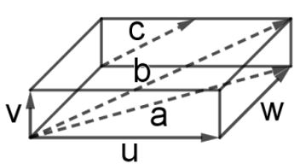
b)
Gegeben sind die Vektoren u (Breite), v (Höhe) und w (Länge). Stelle die Vektoren , und mit Hilfe von , und dar.
c)
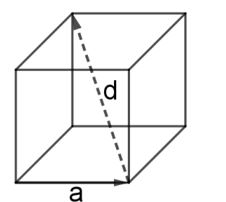
c)
Gegeben ist ein Würfel. Vektor beschreibt eine Kante, Vektor d die Raumdiagonale. Zeige: Die Länge des Vektors entspricht -mal Länge des Vektors a.
Linearkombinationen
a)
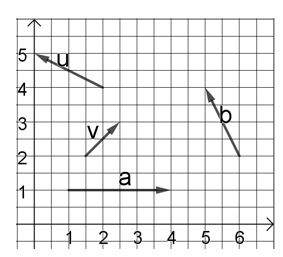
a)
Stelle die Vektoren und als Linearkombination der Vektoren und dar.
b)
Gegeben sind die Vektoren =(2|1|0) und =(-3|0|1). Stelle den Vektor =(0|3|2) als Linearkombination von a und b dar. Zeige, dass man den Vektor =(1|1|1) nicht als Linearkombination von a und b darstellen kann. (Hinweis: Die kleinen Buchstaben sind Vektoren - das sieht man an den Pfeilen - die Zahlen müssen also untereinander geschrieben werden)
Betrag eines Vektors
Gib alle Werte für x an, sodass der Vektor =(1-x|1+x|-4) die Länge 10 hat. (Auch hier werden die Koordinaten werden untereinander geschrieben)
b) Bestimme alle Werte für k so, dass das Dreieck ABC gleichschenklig ist. A(0|1|0), B(4|4|3), C(k|1|0)