Umkehrfunktionen
Was ist eine Umkehrfunktion?
Eine Umkehrfunktion macht das, was eine Funktion macht, wieder rückgängig.
Die Funktion macht zum Beispiel aus einer eine . Die Umkehrfunktion von ist Wenn man die als Argument für die Umkehrfunktion von einsetzt, dann erhält man wieder die .
Wenn die Umkehrfunktion von ist, dann ist auch die Umkehrfunktion von
Bezeichnungen von Umkehrfunktionen
Es gibt unterschiedliche Bezeichnungen für Umkehrfunktionen. Die Umkehrfunktion einer Funktion wird in manchen Büchern oder auf manchen Taschenrechnern als oder bezeichent oder manchmal auch als bzw. .
Bei der Bezeichnung muss man beachten, dass die kein Exponent ist, sondern ein Teil des Namens. Es gilt also nicht
Funktionsgraphen von Umkehrfunktionen
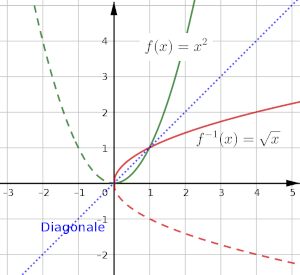
Der Funktionsgraph einer Umkehrfunktion entsteht, wenn man die Abszisse und die Ordinate eines Koordinatensystems einfach vertauscht.
Man kann auch sagen, der Funktionsgraph einer Umkehrfunktion entsteht, indem man den Funktionsgraphen von an der Diagonalen spiegelt, die durch den ersten und den dritten Quadranten des Koordinatenkreuzes verläuft:
Exponentialfunktionen und Logarithmus
Die Umkehrfunktion einer Exponentialfunktion heißt Logarithmusfunktion (sprich: Logarithmus von zur Basis ).
Dann ist natürlich umgekehrt auch die Umkehrfunktion einer Logarithmausfunktion die Exponentialfunktion zur entsprechenden Basis.
Im folgenden Geogebra-Applet können die Funktionsgraphen der Exponential- und Logarithmusfunktionen angesehen werden, deren Basis zwischen und liegt. Die Basis lässt sich mit dem Schieberegler verändern. Außerdem sind "als Referenz", die e-Funktion und der natürliche Lograrithmus abgebildet.
Weil die Exponentialfunktion keine negativen Funktionswerte hat, sind Logarithmusfunktionen bzw. für alle nicht definiert.
Das heißt das Ergebnis von z.B. existiert nicht. Wenn man so etwas in den Taschenrechner eingibt, dann erscheint eine Fehlermeldung.
Berechnen von Umkehrfunktionen
Ist eine Funktion gegeben, dann erhält man die Umkehrfunktion, indem man diese Gleichung nach auflöst, also . Nach dieser Rechnung ist die Variable dann das .
Beispiel:
D.h. die Umkehrfunktion von hat die Funktionsgleichung
Es gibt viele Funktionen, die nicht über den gesamten Definitionsbereich umkehrbar sind. Dann hilt man sich oft damit, dass man nur einen Ausschnitt des Definitionsbereiches betrachtet. Ein Beispiel dafür ist bereits die oben abgebildete Funktion . Man kann hier nur für alle oder für alle die Umkehrfunktion bilden (im Bild oben jeweils die gestrichelte oder die durchgezogene Linie).