Übungsstunde Skalarprodukt von Vektoren, Winkelberechnung
Beim letzten Mal haben wir bereits besprochen, wie du das Skalarprodukt zweier Vektoren und damit deren eingespannten Winkel berechnen kannst. Hier knüpfen wir heute noch einmal an.
Warm-up
Berechne den Winkel, den die Vektoren und miteinander einschließen.
Wie du weißt, ist der Mathematiker an sich sehr effizient und hat hier schnell einen Satz gefunden, um sich Arbeit zu sparen. Gibs also zu! Hast du das Produkt der Beträge noch berechnet?
Halte folgenden Satz in deinem Heft fest und sieh dir die kurze Erklärung an. Vorsicht! Natürlich gilt das ganze nur, wenn keiner der beiden Vektoren der Nullvektor ist.

Hinweis: orthogonal bedeutet senkrecht, rechtwinklig
Üben wir das gleich mal mit einer Basisaufgabe. Hier kannst du dir also Arbeit sparen und nur prüfen, welche der jeweiligen Skalarprodukte Null ergeben (..anstatt auch alle Beträge zu berechnen).
Buch S. 109

Lösung Tipp: Gehe bei solchen Aufgaben systematisch vor. Kombiniere erst alle Vektoren mit a usw.
Wir steigern das Niveau mit dieser Fortgeschrittenenaufgabe. Bei der folgenden Aufgabe musst du jeweils einen Wert so bestimmen, dass die zwei Vektoren orthogonal zueinander sind. Versuche es zunächst selbst. Die Lösung findest du im Video.
Buch S. 109

Weiter geht's mit der nächsten Aufgabe. Teilaufgabe b) ist dabei freiwillig.
Tipp: Stelle ein Gleichungssystem auf.
Buch S. 109

Lösung
Es gibt noch weitere besondere Eigenschaften für das Skalarprodukt. Halte die folgenden beiden in deinem Heft fest und mache dir bewusst, warum sie gelten.
Tipp: Nutze dabei die Definition . Was muss bei einem Bruch gelten, damit das Ergebnis 1 ist?

Üben wir unser neu erlangtes Verständnis über das Skalarprodukt in den folgenden Verständnisfragen.
Buch S. 109

a) Tipp: Achte darauf, ob alle Voraussetzungen gegeben sind.
b)
c)
d)
In Aufgabe d) siehst du den Satz des Pythagoras in vektorieller Form. Diesen und seine Umkehrung kannst du auch mit Hilfe des Skalarproduktes beweisen.
freiwillige Zusatzaufgabe:
Beweise den Satz des Pythagoras mit dem Skalarprodukt. Sende mir deinen Beweis via Chat und ich korrigiere ihn für dich. (siehe S.109/14)
S. 109 Nr. 17
Begründen Sie mithilfe des Skalarproduktes: In einem Parallelogramm mit gleich langen Seiten stehen die Diagonalen senkrecht aufeinander.
Tipp: Stelle zunächst den Vektor w und den Vektor e in Abhängigkeit von Vektor a und d dar. Verwende dann das Skalarprodukt um zu zeigen, dass diese Vektoren aufeinander senkrecht stehen.
Einer Beweisaufgabe wollen wir uns heute noch zusammen widmen. Versuche es zuerst selbst und sieh dir dann die Lösung an.
Tipp:
1. Wir befinden uns in einem Kreis mit Radius r, d.h. alle Vektoren die bei M starten und an der Kreislinie enden, haben die Länge r.
2. Das Distributivgesetz gilt. Stichwort: Binomische Formel.
Buch S. 110
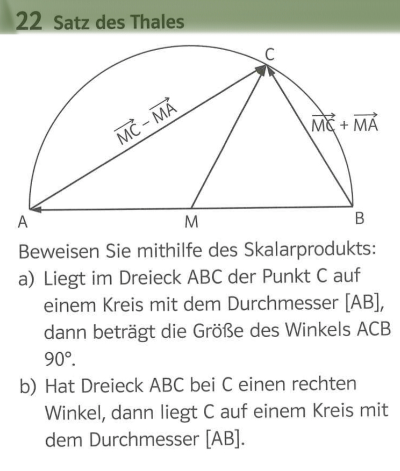
Lösung
Hausaufgabe: Löse das Arbeitsblatt "Skalarprodukt" und bearbeite Nr. 19 auf S. 110.
Hinweis 19a: lege das Dach so in das Koordinatensystem, dass der First über der x-Achse liegt und nur im positiven x-Bereich.
Arbeitsblatt: Skalarprodukt
Freiwillige Zusatzübung:
