El comando Descubrir
Esta actividad pertenece al libro de GeoGebra Inclinando la botella de Piaget con GeoGebra Discovery.
En esta sección usaremos Discovery para demostrar los resultados obtenidos en las posiciones 1 y 2 de la botella de Piaget. Como ello implica establecer relaciones entre distintas áreas (productos de longitudes), vamos antes a ver un ejemplo de uso del comando Descubrir, que solo admite un punto como argumento.
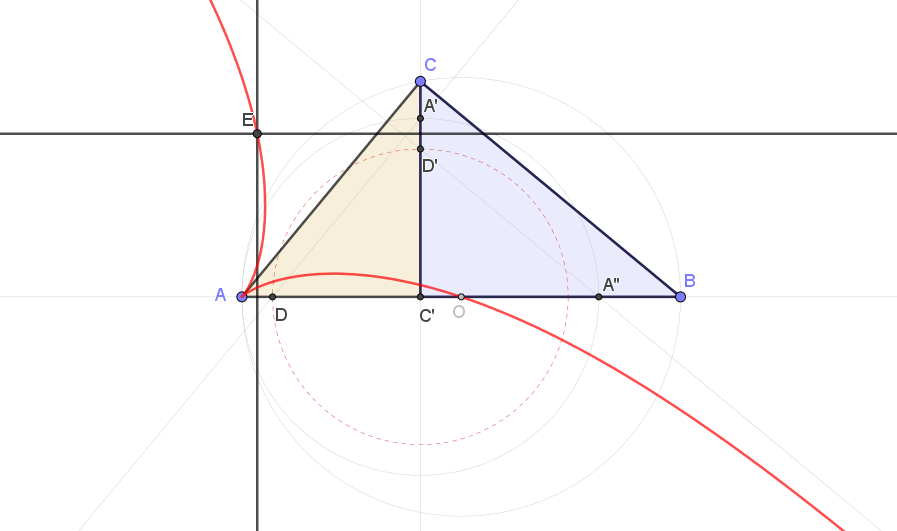
Este comando se encarga de descubrir todas las relaciones de paralelismo, colinealidad, congruencia, etc. entre puntos o segmentos en los que el punto P participa. Sin embargo, gracias al teorema de Tales podemos transformar una relación entre productos o cocientes de longitudes en una relación de congruencia. Como ejemplo, usaremos nuevamente el conocido teorema de la altura. En la siguiente construcción, correspondiente a este teorema, hemos añadido los siguientes pasos:
- Con centro C', trazamos la circunferencia por A y obtenemos A' y A''.
- Trazamos la paralela por A' a AC y obtenemos D.
- Trazamos la paralela por A'' a BC y obtenemos D'.
Así que a/c = c/b si y solo si C'D es congruente con C'D'.
Ahora ya podemos abrir Discovery para ver cómo el comando Descubrir nos permite demostrar el teorema de la altura.
Abrimos GeoGebra Discovery y desde esa página buscamos la URL de esta actividad (https://www.geogebra.org/m/hpzpfgsf). [Alternativamente, también podemos descargar previamente la construcción en nuestro ordenador, pulsando aquí.] GeoGebra Discovery abrirá la construcción que contiene, que es la que aparece arriba. Introducimos:
Descubrir(D)
Observemos que D es uno de los puntos que aparece en la relación C'D'=C'D que queremos demostrar.
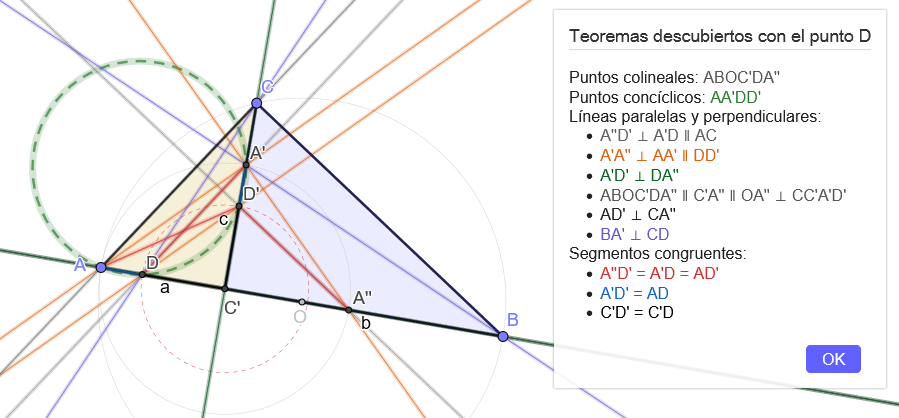
Discovery nos devuelve todas las relaciones que ha encontrado que implican al punto D. Y, efectivamente, la última relación de congruencia que devuelve en el recuadro es justamente la que deseábamos demostrar.
Pero observemos que el comando Descubrir hace honor a su nombre: aparecen otras muchas relaciones, algunas evidentes por construcción, pero otras no tanto. Por ejemplo, muestra que los puntos A, A', D y D' siempre están en la misma circunferencia, lo que invita a seguir explorando la construcción para responder a nuevas preguntas, por ejemplo: ¿dónde se sitúa el centro (E) de esa circunferencia?
Naturalmente, ha de situarse en la intersección de las mediatrices de AD y de A'D', pero también en la mediatriz de AA' y de DD', es decir, la bisectriz del ángulo . Dado que ese centro está determinado por la posición de C en la circunferencia de diámetro AB, podemos averiguar, con el comando EcuaciónLugar, la ecuación del lugar (en rojo en la siguiente imagen) que recorre E al variar C... ¡Algo que ya no tiene nada de evidente!
m = Mediatriz(A, D)
n = Bisectriz(A, C', C)
E = Interseca(m, n)
EcuaciónLugar(E, C)
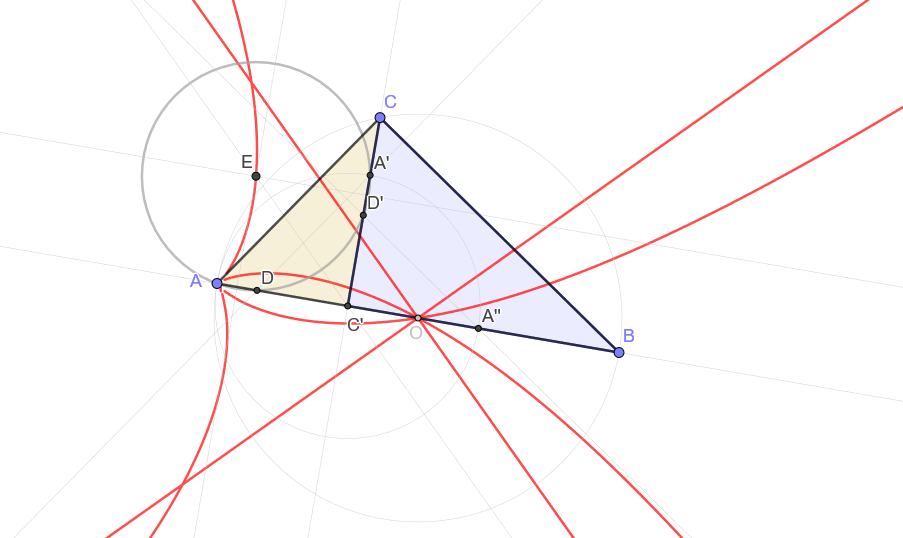
Si tomamos A=(-1, 0) y B=(1, 0), la ecuación que devuelve Discovery es:
ec1: x⁸ + 4x⁷ + 6x⁶ - 8x⁵ y² + 4x⁵ - 2x⁴ y⁴ - 26x⁴ y² + x⁴ - 4x³ y⁴ - 28x³ y² + 14x² y⁴ - 10x² y² + 8x y⁶ + 24x y⁴ + y⁸ + 6y⁶ + 9y⁴ = 0
Vemos que aparecen en el lugar geométrico (debido a simetrías y degeneraciones) más puntos de los que realmente recorre E. GeoGebra nos ayudará a desenlazar esos lugares. Introducimos:
Factoriza(PrimerMiembro(ec1))
que nos devuelve este resultado:
(x - y) (x + y) (x³ - x² y + 2x² + x y² - 4x y + x - y³ - 3y) (x³ + x² y + 2x² + x y² + 4x y + x + y³ + 3y)
Así, averiguamos que el lugar geométrico es la cúbica:
x³ + x² y + 2x² + x y² + 4x y + x + y³ + 3y = 0