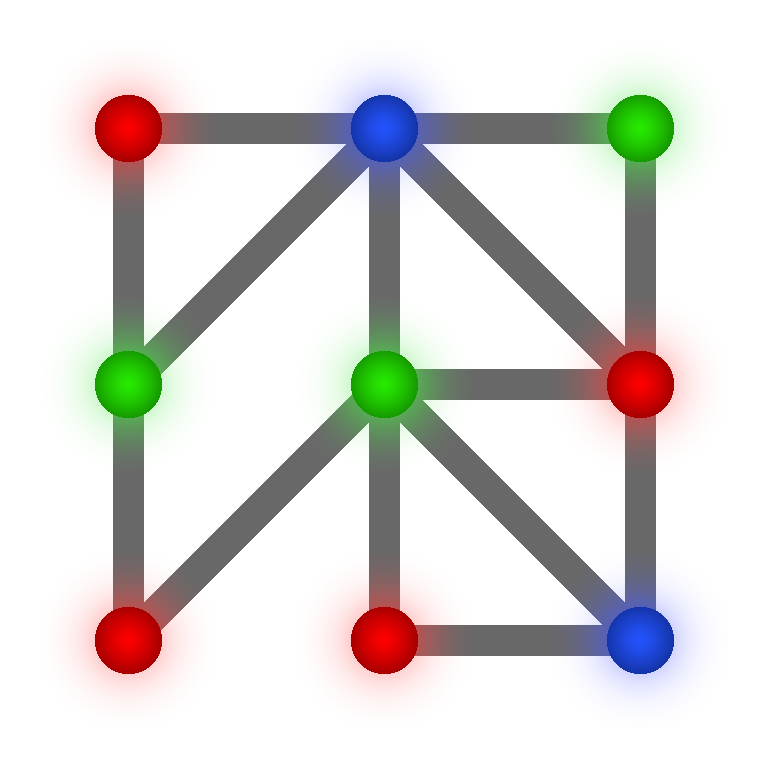
Graafit, ja vaaralliset kemikaalit

YLEISTÄ GRAAFEISTA
MAA11-kurssilta tuttua asiaa ovat monet Diskreetin matematiikan käsitteet. Wikipedia listaa diskreetin matematiikan sateenvarjon alle seuraavia osa- ja sovellusalueita ( https://fi.wikipedia.org/wiki/Diskreetti_matematiikka )
logiikka
joukko-oppi
lukuteoria
verkko- eli graafiteoria
algoritmi
informaatioteoria
laskettavuus- ja kompleksisuusteoria
todennäköisyyslaskenta
lineaarialgebra
peliteoria
diskreetti geometria ja diskreetti topologia
kryptologia ja kryptografia
Kurssin puitteissa tulevat tutuksi monet aiheet logiikan, joukko-opin, lukuteorian ja algoritmiikan kentiltä. Kurssilla käsittelemiemme matemaattisten työkalujen avulla voimme melko helposti lähestyä vielä yhtä diskreetin matematiikan sovelluskohdetta tuolta listalta: graafeja. Käydään lyhyesti läpi muutamia graafeihin liittyviä käsitteitä, ja lopuksi ratkaistaan arkielämän pulmatilanne, jonkatyyppisiin graafeja voidaan hyvin käyttää. Päädymme "värittämään" graafin, vaikka esitetty reaalielämän tapaus ei liity värittämiseen mitenkään.
Mietitään ensin tilannetta, jossa meillä on N kappaletta jotakin alkioita. Nämä voivat periaatteessa olla mitä tahansa, ja matematiikka abstraktina tieteenä sallii näiden alkoiden/objektien olla mitä vain. Esimerkin nimissä katsotaan alla näkyvää kuvaa: joukon alkiot ovat ihmisiä. Alkioiden välille voidaan muodostaa "relaatioita" eli suhteita. Yksinkertaisin suhteiden joukko on Boolen algebran kaltainen; suhde joko on olemassa tai ei ole. Alla näkyvässä kuvassa punaiset viivat ovat ystävyyssuhteita.
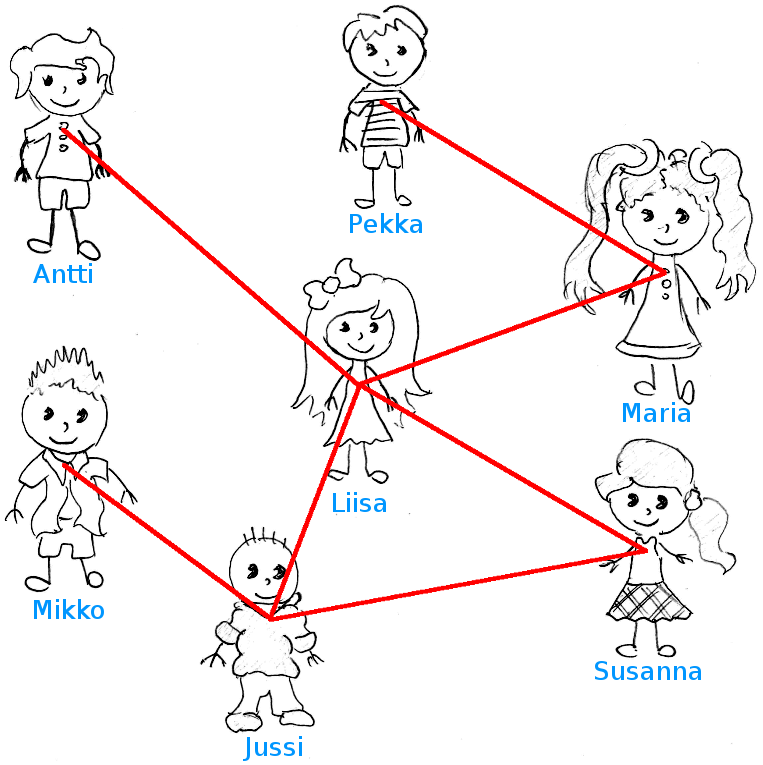
Tässä nähdään graafien voima: niiden avulla voidaan pukea erittäin hyvin visuaaliseen ja ihmisen intuitiiviseen mieleen vetoavaan muotoon tieto siitä, mitkä ovat jotkut objektit, ja miltä näyttävät suhteet näiden välillä. Jos ilmaisisimme saman tiedon ilman visuaalista kuvaa, kuvaus menisi suunnilleen näin:
Määrittelemme seuraavan joukon: {Antti, Pekka, Maria, Liisa, Mikko, Jussi, Susanna}. Näiden alkioiden välillä on seuraavat relaatiot: {Antti-Liisa, Pekka-Maria, Maria-Liisa, Mikko-Jussi, Jussi-Liisa, Jussi-Susanna, Liisa-Susanna}. Tästä esitystavasta on paljon hankalampi saada selvää. Joukkojen ja relaatioiden käsittely voisi mennä pidemmälle; yksi käsiteltävä aihe olisivat tapaukset, jossa relaatiot tapahtuvatkin kahden eri joukon välillä. Katso alla oleva kuva.
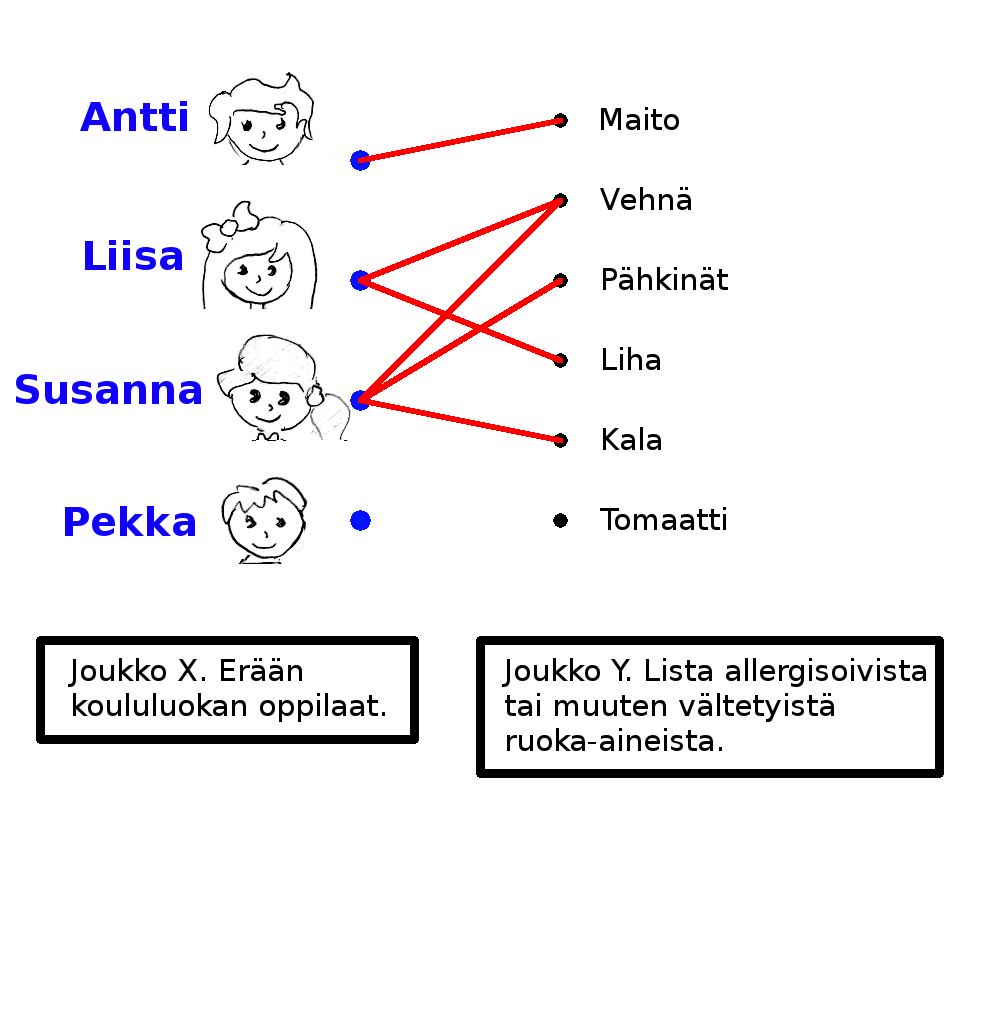
Emme mene tämäntyyppisiin tapauksiin kuitenkaan nyt pidemmälle, vaan katsomme graafeja. Graafit siis koostuvat yhdestä alkioiden jousta, ja relaatioista niiden välillä (niinkuin esimerkki kaveripiiristä). Yleinen kuva graafista annettiin heti otsikon alla.
Katsotaan nyt erästä graafien erityispiirrettä. Tarkastelemalla yksinkertaisia graafeja huomaamme niissä mielenkiintoisen ominaisuuden.
Voimme jokaisen graafin kohdalla kysyä tämän kysymyksen: Jos tahdomme määrittää jokaiselle solmulle jonkun värin, ja vierekkäisillä solmuilla ei saa olla samaa väriä, mikä silloin on
minimimäärä värejä, jonka voimme valita? Kutsumme tätä lukua graafin väriluvuksi (chromatic number). Katsotaan alla olevia kuvia, ja huomatan, että kumpaakaan näistä graafeista ei voisi värittää yhtään vähemmälle määrällä värejä. Toisaalta, enempääkään ei tarvita. Näin ollen kummankin graafin väriluku on neljä. Tätä prosessia kutsutaan “värittämiseksi”, koska sitä käytettiin ensimmäistä kertaa maiden karttoja piirrettäessä.
KONKREETTINEN ESIMERKKI
Graafin “värittämiseen” liittyvissä probleemissa ei toki useinkaan ole
kyse väreistä. Tarkastellaan nyt erästä reaalielämän esimerkkiä. Jos tämä esimerkki olisi esitetty kenelle tahansa meistä muussa aiheyhteydessä, kuin graafeista puhuttaessa, eivät graafit varmaankaan olisi tulleet ensimmäisenä mieleen tästä kysymyksenasettelusta. Käy kuitenkin ilmi, että graafit ja nimenomaan graafin väriluku tarjoavat suoran työkalun vastata tämänkaltaisiin tapauksiin
Kysymys on siis tämä:
Oletetaan, että jokin kemikaaleja tuottava yhtiö kuljettaa tuotteitaan junalla tehtaaltaan tilaajalle. Jotkut kemikaalit reagoivat keskenään tuhoisalla tavalla, jos ne joutuisivat kontaktiin (syttyisivät tuleen, muodostaisivat myrkyllisiä yhdisteitä, tms). Näin ollen niitä ei uskalleta kuljettaa samassa junakuljetuksessa.
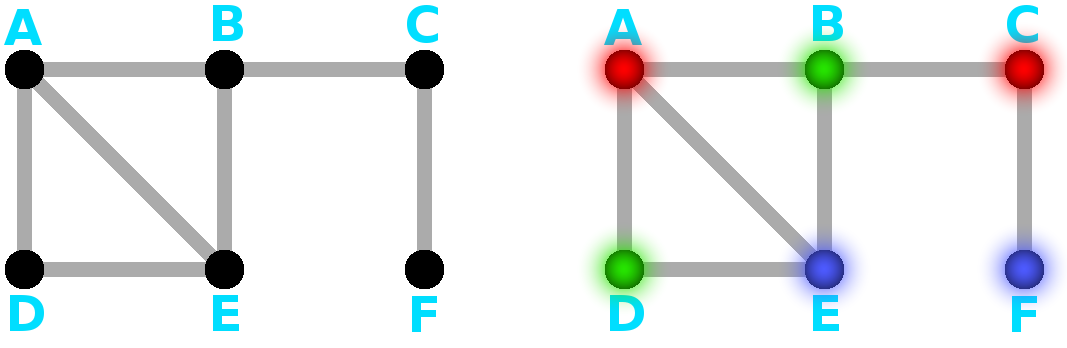
Katsotaan vasemmanpuoleista kuvaa. Oletetaan, että kuljetettavana
on kuutta eri ainetta, ja mikäli solmujen X ja Y välissä on kaari, se
tarkoittaa, että nämä aineet reagoisivat vaarallisesti keskenään.
Kysymys kuuluu, kuinka monella eri junakuljetuksella näitä
kemikaaleja on kuljetettava?
Oikeanpuoleinen kuva on vastaus tähän kysymykseen. Nyt yksi väri
tarkoittaa yhtä junaa; tarvitsemme siis 3 erillistä kuljetusta. Tarkastele väritettyä graafia, ja perustele itsellesi, miksi graafin värittäminen tällä tavalla vastaa tapa kuljettaa kemikaalit turvallisesti.
Haluatko pohtia monimutkaisempaa tapausta? Katso alla olevaa graafia. Jos tämä graafi edustaisi yhdeksää kemikaalia, ja niiden välillä tapahtuvia vaarallisia reaktioita, monellako kuljetuksella kemikaalit nyt pitäisi kuljettaa?
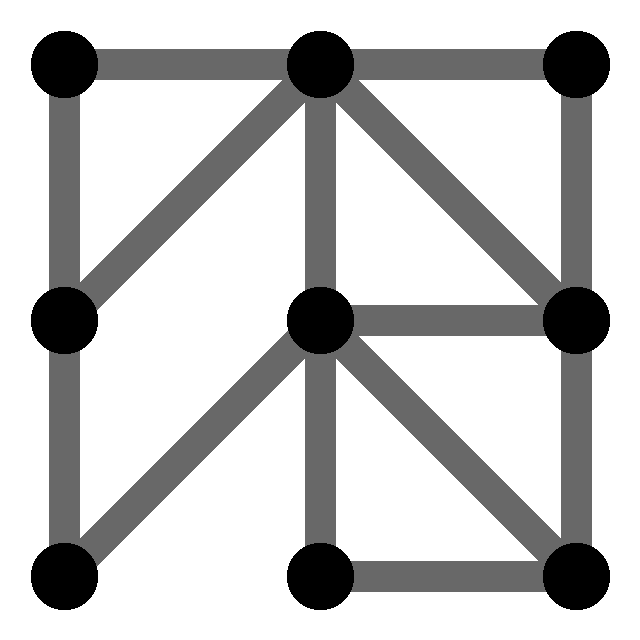
Kuinka pieneksi voit pudottaa graafin väriluvun? Voit ensin itse pohdittuasi poimia ratkaisun alhaalta. Väriluku saadaan sopivalla pohtimisella pudotettua alemmas, kuin alunperin luulisi. Algoritmiikan puolesta mielenkiintoinen ajatus on se, että ei ole olemassa mitään yleispätevää algoritmia, joka etsisi graafin väriluvun.