ZKOUŠKA VZDÁLENOST BODU OD PŘÍMKY V PROSTORU
- Autor:
- Eliška Benešová
- Téma:
- Přímky
ZADÁNÍ
Určete vzdálenost d bodu P od přímky AB.
, ,
POSTUP
1. Bodem P vedeme rovinu kolmou k přímce p
2. Sestrojíme průsečík Q přímky a roviny
3. Vypočteme vzdálenost dvou bodů P a Q
ŘEŠENÍ
Proto abychom mohli vytvořit rovinu, která zahrnuje bod P a je kolmá k přímce p(AB), potřebujeme směrový vektor AB. Směrový vektor AB přímky p je současně normálový vektor roviny.
Přímka p je určena směrovým vektorem a body a .
Její parametrické vyjádření vypadá následovně:
Rovinu vyjádříme obecnou rovnicí takto:
Nyní dosadíme do rovnice bod P.
Průsečík Q roviny a přímky zjistíme vyřešením soustavy rovnic. Parametrické vyjádření přímky dosadíme za neznámé x, y, z do obecné rovnice roviny.
Průsečík Q dopočítáme dosazením parametru do parametrické rovnice přímky p.
Nakonec určíme vzdálenost dvou bodů a tím je úloha vyřešena.
Vzdálenost bodu P od přímky je tedy jednotek.
Jaká je vzdálenost d mezi plotem a patníkem? Projede místem auto široké 2,1 jednotek (m)?
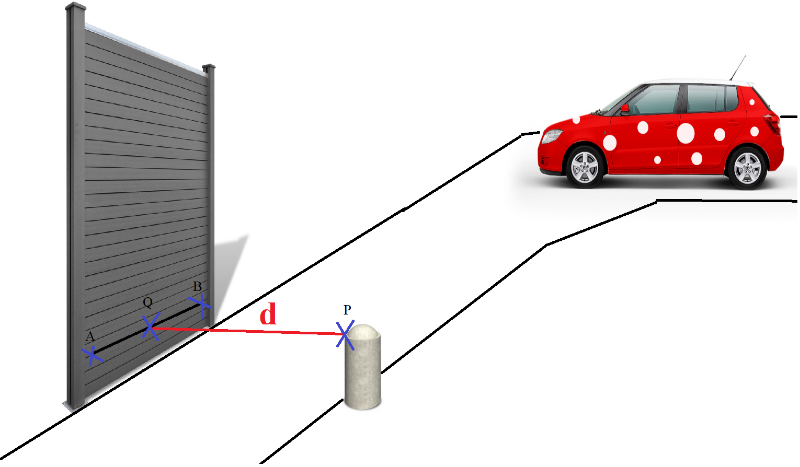
Lze úloha řešit i jiným způsobem?
Určete vzdálenost d bodu P od přímky AB.