Taylor Series
Expressing and Approximating Functions Using the Taylor Series
t’s important to understand the difference between expressing a function as an infinite series and approximating a function by using a finite number of terms of series. You can think of a power series as a polynomial with infinitely many terms (Taylor polynomial).Every Taylor series provides the exact value of a function for all values of x where that series converges. That is, for any value of x on its interval of convergence, a Taylor series converges to f(x).Here’s the Taylor series in all its glory:
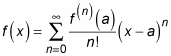In practice, however, adding up an infinite number of terms simply isn’t possible. Nevertheless, you can approximate the value of f(x) by adding a finite number from the appropriate Taylor series. An expression built from a finite number of terms of a Taylor series is called a Taylor polynomial, Tn(x). Like other polynomials, a Taylor polynomial is identified by its degree. For example, here’s the fifth-degree Taylor polynomial, T5(x), that approximates ex:
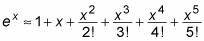Generally speaking, a higher-degree polynomial results in a better approximation. For the value of ex when x is near 100, you get a good estimate by using a Taylor polynomial for ex: with a = 100:
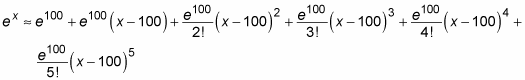To sum up, remember the following:
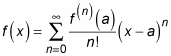In practice, however, adding up an infinite number of terms simply isn’t possible. Nevertheless, you can approximate the value of f(x) by adding a finite number from the appropriate Taylor series. An expression built from a finite number of terms of a Taylor series is called a Taylor polynomial, Tn(x). Like other polynomials, a Taylor polynomial is identified by its degree. For example, here’s the fifth-degree Taylor polynomial, T5(x), that approximates ex:
Generally speaking, a higher-degree polynomial results in a better approximation. For the value of ex when x is near 100, you get a good estimate by using a Taylor polynomial for ex: with a = 100:
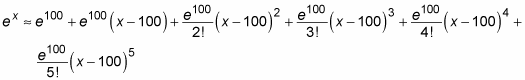To sum up, remember the following:- A convergent Taylor series expresses the exact value of a function.
- A Taylor polynomial, Tn(x), from a convergent series approximates the value of a function.