Teorema del sándwich
En esta página enunciamos el teorema del emparedado (sin demostración) y lo aplicamos para calcular el límite de la función sin(x)/x cuando x tiende a infinito positivo.
1. Introducción
El teorema del emparedado o del sándwich es un teorema que permite calcular el límite de funciones que se encuentran acotadas por otras dos funciones cuyos límites son iguales.
Se trata de un resultado muy intuitivo y existen varias versiones (para sucesiones, series, funciones con varias variables, etc.).

2. Teorema del sándwich o del emparedado
Sean g, f y h funciones definidas en el intervalo I que contiene al punto a tales que
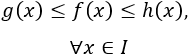 Supongamos también que
Supongamos también que
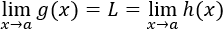 Entonces,
Entonces,
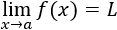 Nota: las funciones pueden no estar definidas en el punto a.
Nota 2: L debe ser finito.
Nota: las funciones pueden no estar definidas en el punto a.
Nota 2: L debe ser finito.
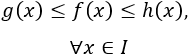 Supongamos también que
Supongamos también que