E07 Szabályos ötszög - háromszög átdarabolás
Kapcsolatok
Mint itt láttuk, a Wallace-Bolyai-Gerwien-tétel 1807-es bizonyítását követően -1903-ban mutatott először példát H.E. Dudeley arra, hogy egy négyzetet miként lehet négy részre osztva átdarabolni szabályos háromszöggé.
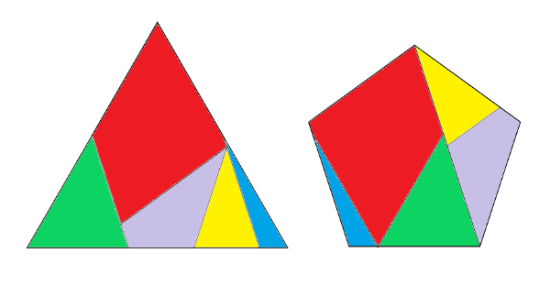
1951-ben láthattak példát a matematikusok - és a rejtvényfejtők - arra, hogy miként lehet egy szabályos ötszöget hat részre vágva átdarabolni szabályos háromszöggé.
Vajon ez az átdarabolás "csak" puzzle-ként helyes, vagy matematikailag is pontos?
6 részes puzzle 1. változat: Michael Goldberg 1951.
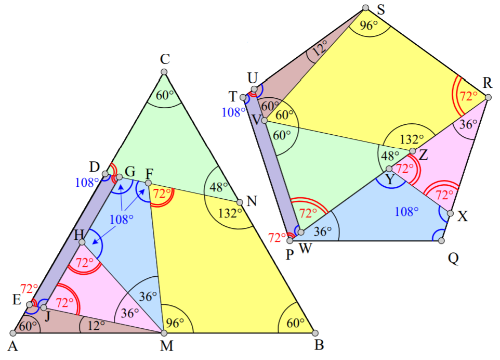
Ugyanez a kérdés az alábbi átdarabolások esetében is. Ezeket a szerkesztéssel előállított átdarabolásokat - egyelőre - csak rajzokon mutatjuk be, a problémák alaposabb elemzését olvasóinkra bízzuk.
6 részes puzzle 2. változat
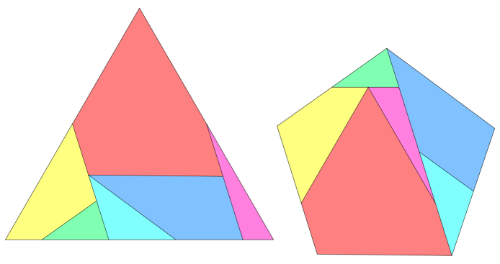
6 részes puzzle, 3 . változat
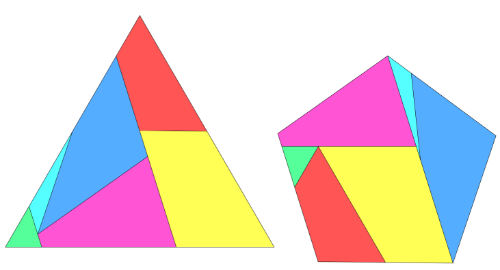
5 részes puzzle