Bisectriz e incentro
La bisectriz de un ángulo es la semienta que divide al ángulo en dos partes iguales.
Propiedad: Para cualquier punto de la bisectriz, su distancia (mas corta) a cada uno de los lados del ángulo es la misma.
Por la propiedad anterior, el punto P está a la misma distancia del los segmentos AB y AC, por lo que es el centro de una circunferencia que es interior a los lados y tangente (solo los interesa en un punto). Para verlo activa la casilla "Ver circunferencia" en la ventana de arriba.
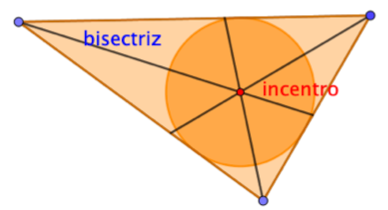
Si se construyen las tres bisectrices de los tres lados de un triángulo se observa que pasan por el mismo punto. Este punto se llama incentro. Como cada bisectriz puede formar estas circunferencias interiores y tangentes, el incentro es el centro de la circunferencia inscrita del triángulo.
Obsérvalo en la siguiente ventana, donde se observa cómo las tres circunferencias interiores y tangentes a los lados se unen en la mayor de ellas: la circunferencia inscrita.
ACTIVIDAD: En la siguiente ventana realiza los siguientes pasos:
- Construye un triángulo ABC.
- Utiliza la herramienta bisectriz
para construir las bisectrices de los 3 ángulos. GeoGebra por defecto dibuja también la bisectriz exterior (perpendicular a la bisectriz usual). Puedes esconderlas por ahora. - Renombra su punto de intersección como el incentro.
- Construye la circunferencia inscrita del triángulo ABC.
Mueve la construcción que acabas de realizar y contesta a las siguientes preguntas:
¿El incentro se encuentra siempre en el interior del triángulo? ¿Por qué?
¿El incentro y la circunferencia inscrita siempre existen? ¿Qué ocurre en las "situaciones límite"?
Como curiosidad, incluye en la construcción las bisectrices exteriores (es decir, no las escondas en el paso 2 anterior). ¿Ves que también se interesan de alguna forma?