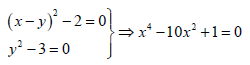13. Radicales y raíces
Investigación: Los números reales, parte 13. Rafael Losada Liste
En la siguiente figura se puede ver la construcción de la suma de dos radicales:
En los últimos ejemplos, hemos construidos números bastante complicados. ¡Pero no los hemos identificado como raíces de ninguna función, ni de ninguna otra forma!
Una cosa es construir y otra cosa es definir.
Sin embargo, todos los ejemplos vistos hasta ahora se pueden definir partiendo de su construcción.
En el siguiente ejemplo, se observa que la suma de raíces cuadradas es una solución de cierto polinomio de
cuarto grado. (Nota: el polinomio se encuentra dividido por una constante simplemente para facilitar su visualización; esto no afecta a sus raíces.)
A continuación se expone la forma de obtener el polinomio que tiene por raíz una suma, resta, producto o cociente de raíces de otros polinomios.
Problema general
Sabiendo que p(x) y q(x) son polinomios y p(a) = q(b) = 0, encontrar los polinomios r(x) que cumplan:
a) r(a+b) = 0
b) r(a-b) = 0
c) r(a b) = 0
d) r(a/b) = 0
Solución general
a) Se plantea el sistema p(x-y) = q(y) = 0, y se elimina y.
b) Se plantea el sistema p(x+y) = q(y) = 0, y se elimina y.
c) Se plantea el sistema p(x/y) = q(y) = 0, y se elimina y.
d) Se plantea el sistema p(x y) = q(y) = 0, y se elimina y.
Ejemplo
Sean p(x)=x2-2 y q(x)=x2-3 . Los números y son, respectivamente, una de sus raíces. Queremos encontrar un polinomio que tenga por raíz su suma: