Manipulation an Funktionsgraphen
Verschiebung in y-Richtung
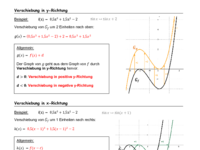
Beispiel:
 Verschiebung von um 2 Einheiten nach oben. Dann erhalten wir
Verschiebung von um 2 Einheiten nach oben. Dann erhalten wir
g(x)=
Allgemein gilt also
Der Graph von g geht aus dem Graphen von f durch Verschiebung in y-Richtung hervor.
Verschiebung in x-Richtung
Beispiel:
 Verschiebung von um 1 Einheit nach rechts. Dann erhalten wir
Verschiebung von um 1 Einheit nach rechts. Dann erhalten wir
g(x)=
Allgemein gilt also
Der Graph von g geht aus dem Graphen von f durch Verschiebung in x-Richtung hervor.
Spiegelung
Beispiel:

Wir spiegeln an der x-Achse und erhalten g(x)=
Wir spiegeln an der y-Achse und erhalten h(x)=
Allgemein gilt also
geht durch Spiegelung von an der x-Achse hervor.
geht durch Spiegelung von an der y-Achse hervor.
Streckung in y-Richtung
Beispiel:


Allgemein gilt also
Der Graph von g geht aus dem Graphen von f durch Streckung in y-Richtung hervor, falls
Streckung in x-Richtung
Beispiel:


Allgemein gilt also
Der Graph von g geht aus dem Graphen von f durch Streckung in x-Richtung hervor, falls
Allgemein geht also die Funktion durch Verschiebungen, Spiegelungen, Streckungen in die Funktion
über.