Eksponentiaalinen populaatio

Vuonna 1859 eräs englannista Australiaan muuttanut uudisasukas pohti, että jänisten metsästys oli ollut Vanhalla Mantereella hauskaa puuhaa, mutta Uudella Mantereella ei jäniksiä edes ollut. Hän ajatteli, että ehkä jänis tulisi toimeen Australian luonnossa, vaikka ei siellä natiivi laji olekaan. Näinpä hän päätti päästää 24 jäniksestä koostuvan populaation vapaaksi takapihallaan.
Jänis on erittäin sopeutunut laji, ja populaatio lähti räjähdysmäiseen kasvuun. Kun jänisten vapauttamisesta oli kulunut 20 vuotta, populaation koko oli noin 7000 yksilöä. No, ei syytä huoleen, kyllä muutama tuhatta jänistä Australian kokoiselle mantereelle mahtuu. Mutta mikä on populaation koko silloin, kun vapauttamisesta on kulunut 70 vuotta?
RATKAISU:
Merkitään jänisten määrää y:llä ja aikaa x:llä. Nyt voimme kirjoittaa populaation koon tietyllä ajanhetkellä alla näkyvän kuvan mukaisesti.
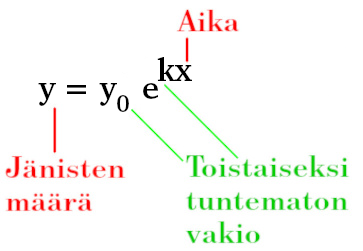
Tässä muodossa e on toki tuttu Neperin luku. Vastaavasti ja ovat toistaiseksi tuntemattomia vakioita, joiden lukuarvon voimme selvittää. Tehtävän ratkaisu lähtee siis siitä, että selvitämme nämä lukuarvot.
Vakioista on helppo selvittää; se on vain populaation koko alussa. Tämä on helppo todentaa, ja tehdään se tässä. Kun käsillä oleva ajanhetki on , sillon myös termi saa lukuarvon yksi, riippumatta :n lukuarvosta. Tällöin .
Nyt, kun tunnemme :n arvon, lähdemme selvittämään :n lukuarvoa. Kirjoitetaan ensin annettu yhtälö, ja lisätään siihen kaikki tunnetut lukuarvot, ja käytetään niitä lukuarvoja, jotka vallitsevat ajanhetkenä . Silloin siis ja .
Otetaan tästä muodosta logaritmi puolittain.
Lasketaan yllä näkyvä lasku auki, ja saadaan :lle arvo 0.28378.
Nyt tiedämme siis, että voimme kirjoittaa jänisen määrän ajan funktiona alla näkyvällä tavalla. Tästä muodosta voimme laskea jänisten määrän millä tahansa ajanhetkellä.
Tehtävässä oli tarkoituksena laskea jänisten määrä 70 vuoden päästä jänispopulaation vapaaksi päästämisestä. Lasketaan
Huomataan, että jänisten määrä on keulinut huikeisiin lukuihin! Saatu luku on melko tarkkaan kymmenen miljardia.