Урок 25
Задача 1
1) Три дороги – магистраль, шоссе и проселочная дорога – образуют треугольник АВС, в котором 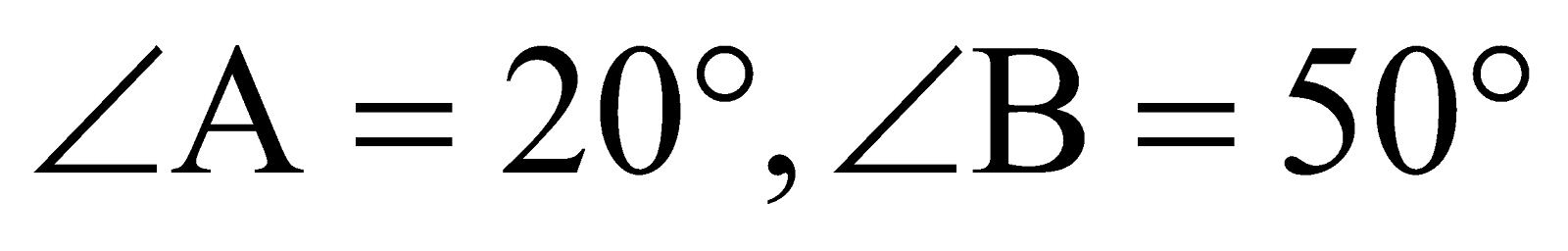 и АВ = 2 км (см. рисунок). Какова длина отрезка АС?
2) в 12.00 нарушитель правил дорожного движения свернул в точке А с магистрали на шоссе и поехал в направлении перекрестка С со скоростью 140 км/ч. В то же время (в 12.00) из пункта В по проселочной дороге в сторону перекрестка С выехал инспектор дорожной полиции и достиг этого перекрестка через 35 секунд. Успел ли инспектор полиции к перекрестку раньше нарушителя? Обоснуйте свой ответ
с помощью вычислений.
и АВ = 2 км (см. рисунок). Какова длина отрезка АС?
2) в 12.00 нарушитель правил дорожного движения свернул в точке А с магистрали на шоссе и поехал в направлении перекрестка С со скоростью 140 км/ч. В то же время (в 12.00) из пункта В по проселочной дороге в сторону перекрестка С выехал инспектор дорожной полиции и достиг этого перекрестка через 35 секунд. Успел ли инспектор полиции к перекрестку раньше нарушителя? Обоснуйте свой ответ
с помощью вычислений.
Дано:
Решение:
1. по теореме синусов
(км)
2. ===0.01 (час)=36 (с) - нарушитель правил доедет до перекрёстка С, значит полицейский приедет туда на 1 секунду раньше.
Ответ: AC=1.6 км; полицейский успеет к перекрёстку раньше нарушителя на 1 секунду.
Задача 3
Диагональ АС параллелограмма АВCD равна 6,7 см, а сторона AD равна 5,4 см.
Угол ACB равен 102 .
1. Отметьте данные на рисунке.
.
1. Отметьте данные на рисунке.
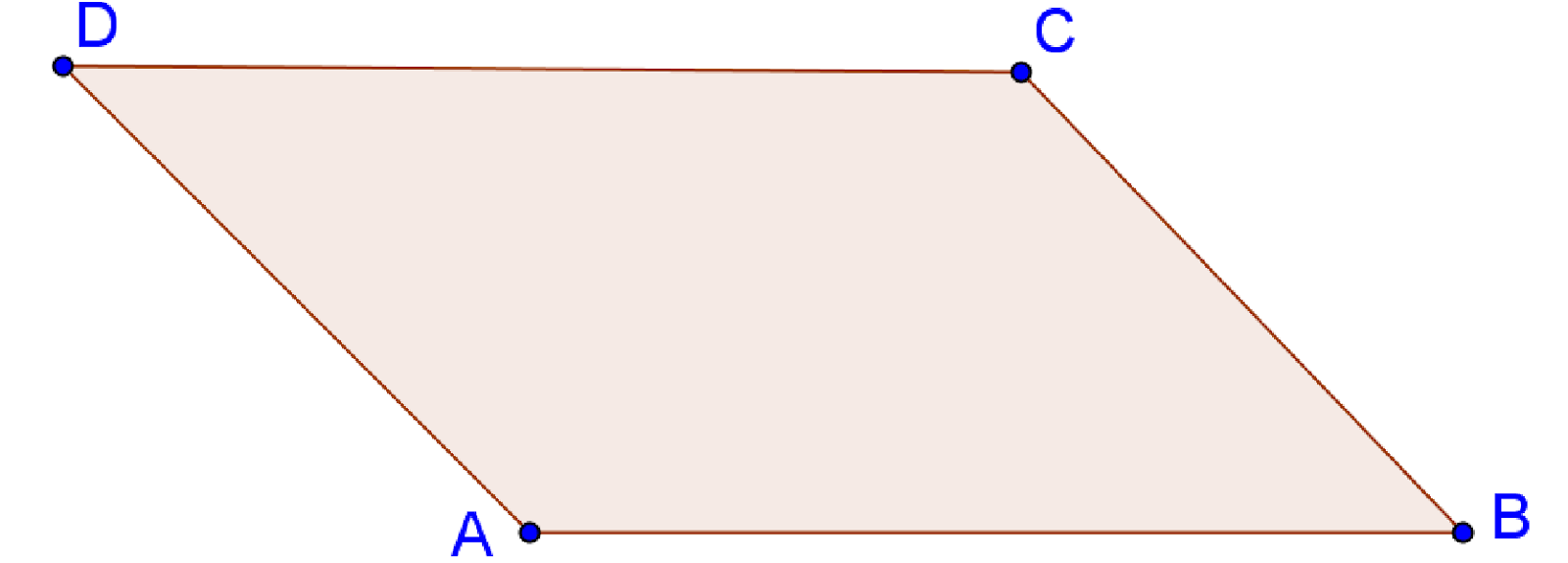 2. Вычислите периметр и площадь параллелограмма ABCD.
3. Биссектриса угла ACB пересекает сторону AB параллелограмма в точке E. Вычислите длины отрезков AE и EB.
NB! Все конечные результаты округлите с точностью до десятых.
2. Вычислите периметр и площадь параллелограмма ABCD.
3. Биссектриса угла ACB пересекает сторону AB параллелограмма в точке E. Вычислите длины отрезков AE и EB.
NB! Все конечные результаты округлите с точностью до десятых.
Дано:
Решение:
1. ΔABC; по теореме косинусов
AB²=AC²+CB²-2×AC×CB×cos∠ACB
AB²=5.4²+6.7²-2×5.4×6.7×cos102
AB=√89.09=9.4 (см)
по теореме синусов
2. P=2(AB+CB)
P=2(9.4+5.4)=29.6 (см)
S=AB×AC×sin∠B=9.4×5.4×0.6972=35.4 (см²)
3. ΔBCE; по теореме синусов
BE==
BE=4.2 (см) AE=AB-BE=9.4-4.2=5.2 (см)
Ответ: P=29.6 см; S=35.4 см²; BE=4.2 см; AE=5.2 см.