elliptische Funktionen 2
Die WEIERSTRAßsche ℘-Funktion auf der RIEMANNschen Zahlenkugel
Diese Seite ist Teil des GeoGebra-Books Moebiusebene. (August 2019)
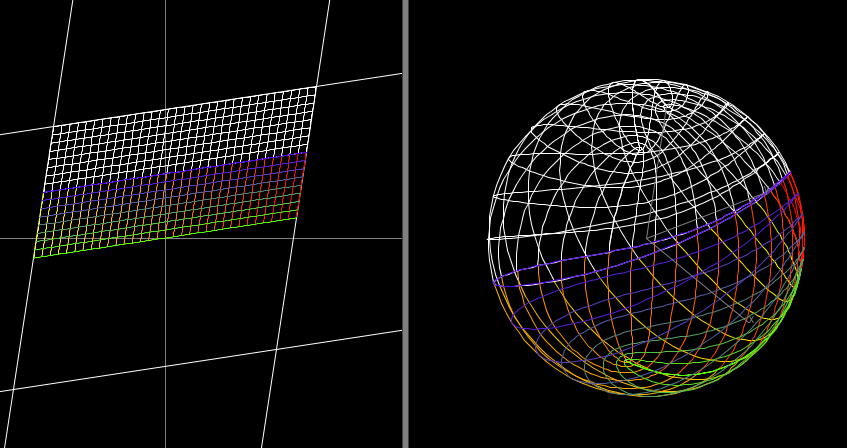
Die Darstellung der WEIERSTAßschen -Funktion oben ist leider nur ein Bild, welches man sich auf http://3d-xplormath.org/j/index.html mit dem dortigen Programm auch bewegt anschauen kann. Weitere Beispiele elliptischer Funktionen findet man auf der sehenswerten Seite http://virtualmathmuseum.org unter den Beispielen für konforme Funktionen. (Siehe auch das Bild unten!) Die Elliptische Funktionen, die wir hier gerne bewegter darstellen würden, sind doppelt-periodische komplex-differenzierbare Funktionen. Ein Parallelogramm wird ganz auf die Kugel abgebildet, 4 Punkte bleiben ausgespart: Nullstellen der Ableitung - für uns sind das die Brennpunkte. Die Funktion wiederholt sich periodisch längs der beiden Parallelen-Richtungen und windet sich um die 4 Brennpunkte. Die parallelen Strecken werden auf geschlossene Kurven um die Brennpunkte abgebildet. Die Funktionen sind konform, also winkeltreu! Möbiusgeometrisch sind diese Funktionen vollständig durch die Lage der 4 Brennpunkte und damit durch deren absolute Invariante bestimmt. *) siehe unten Ist reell, so liegen die Brennpunkte auf einem Kreis , oder spiegelbildlich auf 2 orthogonalen Kreisen . In all diesen Fällen sind die oben erkennbaren geschlossenen Kurven konfokale bizirkulare Quartiken. Im Bild unten sind die geschlossenen Kurven nicht orthogonal, es dürfte ein Beispiel einer elliptischen Funktion mit nicht-reeller absoluten Invariante darstellen! Die RIEMANNsche Zahlenkugel und mit ihr die Bilder der Kurven oder könnte man sich bewegt von allen Seiten anschauen. Der eine Brennpunkt der WEIERSTRAßschen -Funktion hätte dann keine Sonderstellung mehr, aber der Überblick über das geometrische Verhalten der Funktion wäre sicher größer als jede ebene Darstellung! Überhaupt: wir meinen, komplex-differenzierbare Funktionen könnten geometrisch ein lohnendes Thema für ge
gebra sein!
*) das Kapitel Die Lage von 4 Punkten
und 4 Punkte ...
und Die Lage von 4 Punkten, komplex berechnet
und Doppelverhältnis von 4 PunktenElliptische Funktion, auf der RIEMANNschen Zahlenkugel
