5 ways to calculate the area of a triangle
Method 1
Construct a perpendicular line segment from one vertex to the base of the triangle. Calculate the length of the base and of the height to determine the area of the triangle using .
Method 2
Calculate the length of all three sides and use Heron's formula, , where s is the semiperimeter, , of the triangle. Did you get the same answer?
Method 3
Calculate the measure of any angle using the Law of Cosines, , and then use the formula, derived from right triangle trigonometry, . You can use any pair of sides and their included angle. Did you get the same result?
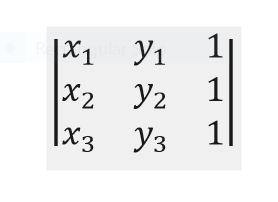
Method 4
Calculate the determinant of the matrix formed by entering the coordinates of points followed by the number 1, as in the image above, in a 3 X 3 matrix. If it is positive, multiply it by and if it is negative, by . Did you get the same result?
Method 5
Construct a rectangle in which the triangle is inscribed. Calculate the areas of the right triangles outside the triangle and subtract them from the area of the rectangle.
Extension to 3-dimensions
Which of the methods above would apply to a triangle in 3-dimensions?
Find the area using the methods you indicated.
Magnitude of the Cross-Product
Find the vector that is perpendicular to the plane containing the triangle.
The area of the triangle is 1/2 the magnitude of this vector.