Optimierungsaufgaben

Mit dem Schieberegler V können Sie das Volumen einer zylindrischen Dose vorgeben.
Anschließend können Sie mit dem Schieberegler r den Radius der Dose variieren.
Die Höhe h und der Flächeninhalt O der Oberfläche ergeben sich dann automatisch.
Variieren Sie den Radius so, dass Sie eine minimale Oberfläche erhalten.
Unten finden Sie ein Video im dem gezeigt wird, wie man den Radius mit der Optimalen Oberfläche findet.
Vielleicht können Sie auch ganz allgemein zeigen, dass die minimale Oberfläche bei einem Radius von
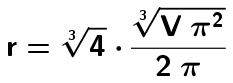
gegeben ist.
Im Tutorial wird gezeigt, wie man den Materialverbrauch für eine zylinderförmige Dose mit vorgegebenen Volumen minimiert.
Bestimmen Sie x0 so, dass der Flächeninhalt des Rechteckes maximal wird.
Diese Aufgabe können Sie nicht rein algebraisch lösen.
Lösung: 1.683624537747