Pendiente de una Recta y ángulo de inclinación
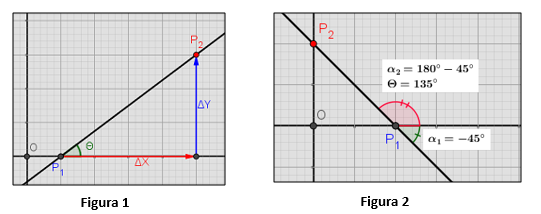
1. Si la pendiente es positiva (m>0), la recta es inclinada ascendente y el ángulo de inclinación θ con relación al semieje X positivo es agudo,es decir, menor que 90°. 2. Si la pendiente es negativa (m<0), la recta es inclinada descendente y el ángulo de inclinación θ con relación al semieje X positivo es obtuso, es decir, mayor que 90° y menor que 180°. 3. Si la pendiente es nula (m = 0), la recta es horizontal y el ángulo de inclinación θ con relación al semieje X positivo es 0°. Este caso se presenta cuando y2 = y1. 4. Si la pendiente de la recta no está definida, la recta es vertical y el ángulo de inclinación θ es de 90°. Este caso se presenta cuando x2 = x1. En el applet active la casilla de verificación características de la recta.