Minimum/Maximum d'une fonction
Geogebra pour visualiser un maximum/minimum
Dans le plan, on considère un carré ABCD de côté 1 cm. Soit E un point du segment [DA].
On place le point F sur la demi-droite [Bx) tel que BF = DE .
On note I le point d’intersection des droites (EF) et (BC).
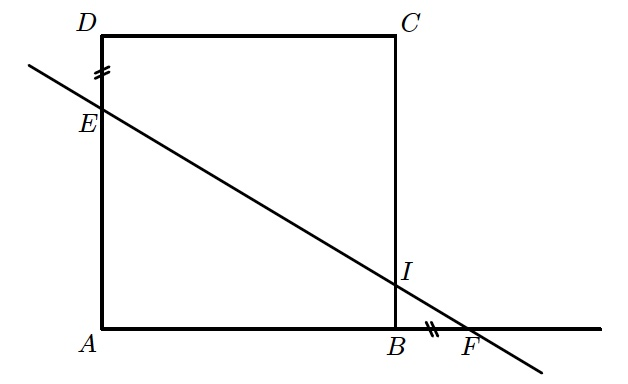
Énoncé possible pour les élèves
On note x la longueur DE et y la longueur BI.
1. A l’aide d’un logiciel de dessin dynamique :
a. Reproduire la configuration ci-dessus en plaçant le point E libre sur le segment [AD].
b. Afficher la courbe composée des points M de coordonnées (x ; y) lorsque x décrit l’intervalle [0;1]
c. Conjecturer une valeur approchée de la longueur DE pour laquelle la longueur BI est maximale.
2. a. Dans le repère ( A; B ; D ) orthonormal, exprimer la longueur IB en fonction de x.
b. On considère la fonction f définie sur [0 ; 1] par :
Déterminer les extrémums de la fonction f sur l’intervalle [0 ; 1]
c. Établir la conjecture faite à la question 1. c.
Indication pour tracer la figure :
1ère partie : dans la partie gauche
1 – Tracer en premier ce qui est fixe : ici le carré ABCD et la demi-droite [AB)
2 – Placer ce qui est mobile : ici le point E mais il sera « lié » au segment [AD]
3 – Construire le point F en reportant la distance DE. Le plus simple est de créé un cercle de centre B et de rayon DE (outil Cercle (centre ; rayon))
3 – Construire le reste de la figure en conservant les propriétés de celle-ci.
2ème partie (point M) : dans la partie gauche
4 – Pour le point M, le plus simple est de créer un point puis de modifier ses paramètres en choisissant comme coordonnées (DE,BI)