Wahrscheinlichkeitsrechnung
Zufallsversuch
Bei einem Zufallsversuch tritt genau eines von mehreren möglichen Ergebnissen ein. Welches Ergebnis dabei genau eintritt, ist nicht vorhersagbar. Es ist nur eine Wahrscheinlichkeit berechenbar, mit der das Ergebnis eintreten kann.
Beispiel:
Wurf eines Würfels
mögliche Ergebnisse: 1, 2, 3, 4, 5, 6
Wurf einer Münze:
mögliche Ergebnisse: Kopf, Zahl
(rein theoretisch kann die Münze auch so geworfen werden, dass sie auf ihrem Rand stehen bleibt - dieser Fall ist aber äußerst selten und damit höchst unwahrscheinlich)
Ereignis
Alle Ergebnisse eines Zufallsversuchs, die eine bestimmte Eigenschaft besitzen, bilden ein Ereignis.
Diese Ergebnisse heißen dann die für das Ergebnis günstigen Ergebnisse.
Die drei Ergebnisse 2; 4; 6 bilde das Ereignis "eine gerade Zahl würfeln".
spezielle Ereignisse
Ein Ereignis, das bei keinem Versuch auftreten kann, heißt unmögliches Ereignis.
Beispiel: Würfeln einer Augenzahl größer als 6. -> das ist nicht möglich
Ein Ereignis, das bei jedem Versuch auftritt, heißt sicheres Ereignis.
Beispiel: Eine der Augenzahlen von 1 bis 6 wird gewürfelt.
Laplace
Laplace-Versuche:
Zufallsversuche, bei denen alle Ergebnisse gleich wahrscheinlich sind, heißen Laplace-Versuche.
Laplace-Wahrscheinlichkeiten:
Hat ein Laplace-Versuch n mögliche Ergebnisse, dann beträgt die Wahrscheinlichkeit für jedes Ergebnis .
Für die Wahrscheinlichkeit P(E) eines Ereignisses E gilt:
Beispiel:
E: Die Augenzahl ist gerade.
Gegenereignis
Alle Ergebnisse, die für ein Ereignis E nicht günstig sind, bilden das Gegenereignis .
Für die Wahrscheinlichkeit gilt:
P(¯E)=1−P(E)
Das Gegenereignis von "eine Sechs würfeln" ist "keine Sechs würfeln".
P(keine Sechs) = 1 - P(Sechs) =
Gesetz der großen Zahlen
Ist ein Zufallsversuch kein Laplace-Versuch, so können die Wahrscheinlichkeiten der möglichen Ergebnisse in der Regel nur geschätzt werden.
Dazu führt man den Versuch möglichst oft durch. Die relative Häufigkeit, mit der ein Ergebnis eintritt, wird als Schätzwert für die Wahrscheinlichkeit dieses Ergebnisses genommen.
Der Schätzwert wird umso zuverlässiger, je mehr Versuche durchgeführt werden.
Mehrstufige Zufallsversuche
Werden mehrere nacheinander ablaufende Zufallsversuche zu einem einzigen Zufallsversuch zusammengefasst, so spricht man von einem mehrstufigen Zufallsversuch.
Der aufeinander folgende Wurf zweier durch ihre Körpernetze beschriebenen Würfel A und B ist ein zweistufiges Zufallsexperiment.
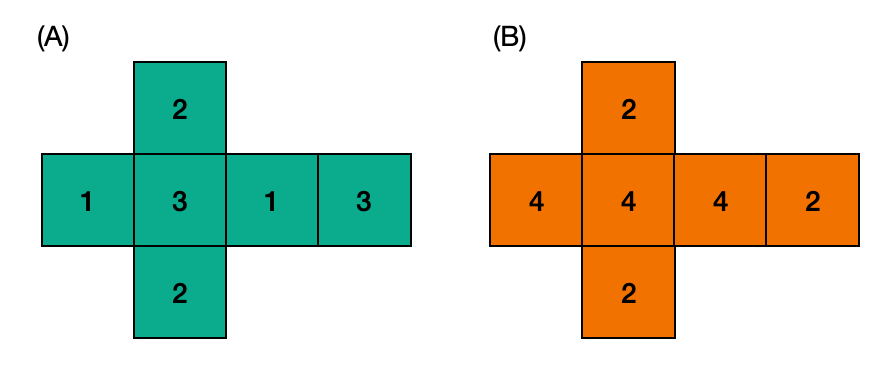
Baumdiagramm
Ein Baumdiagramm veranschaulicht die möglichen Ergebnisse eines mehrstufigen Zufallsversuchs und deren Wahrscheinlichkeit.
Jedem Pfad im Baumdiagramm entspricht genau eine Ergebnis. Ein Ereignis besteht aus einem oder mehreren Ergebnissen, die durch die entsprechenden Pfade dargestellt werden.
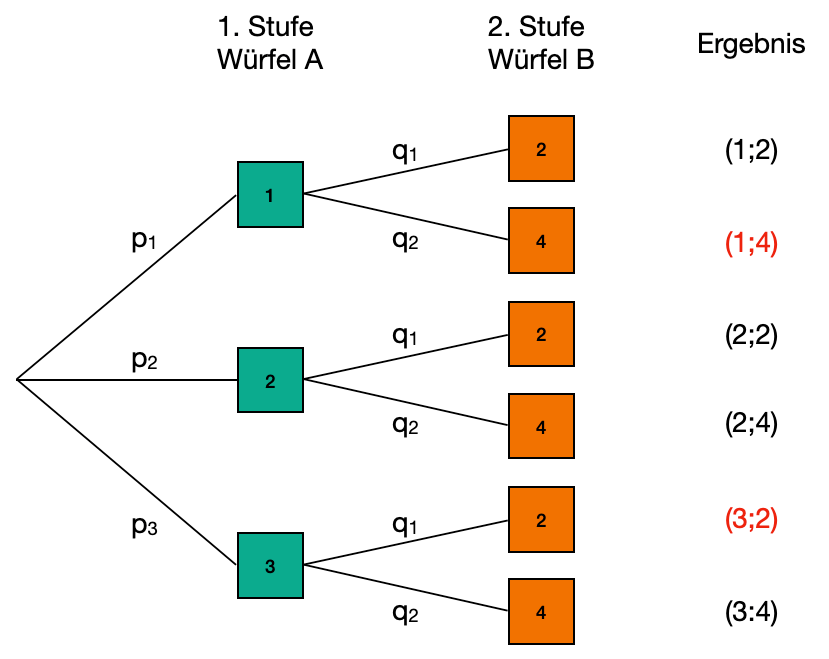
Produktregel (Pfadregel)
(Wahrscheinlichkeit eines Ergebnisses):
Die Wahrscheinlichkeit eines Ergebnisses in einem mehrstufigen Zufallsexperiment ist gleich dem Produkt der Wahrscheinlichkeiten entlang des zugehörigen Pfades im Baumdiagramm.
Beispiel: "Nur 2er"
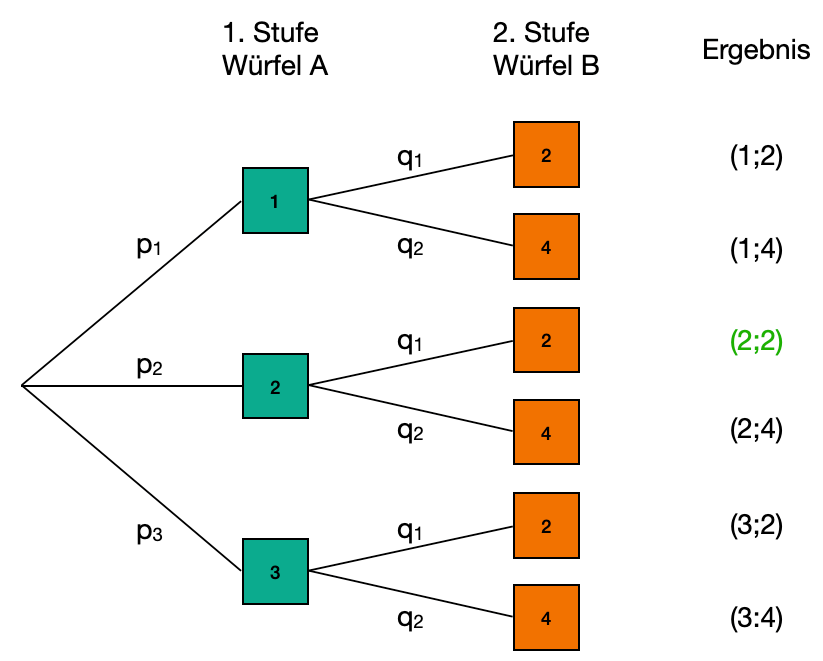
Summenregel
(Wahrscheinlichkeit eines Ergebnisses):
Die Wahrscheinlichkeit eines Ergebnisses in einem mehrstufigen Zufallsexperiment ist gleich der Summe der Wahrscheinlichkeiten aller zu diesem Ereignis gehörenden Pfade im Baumdiagramm.
Beispiel: Augensumme 5.
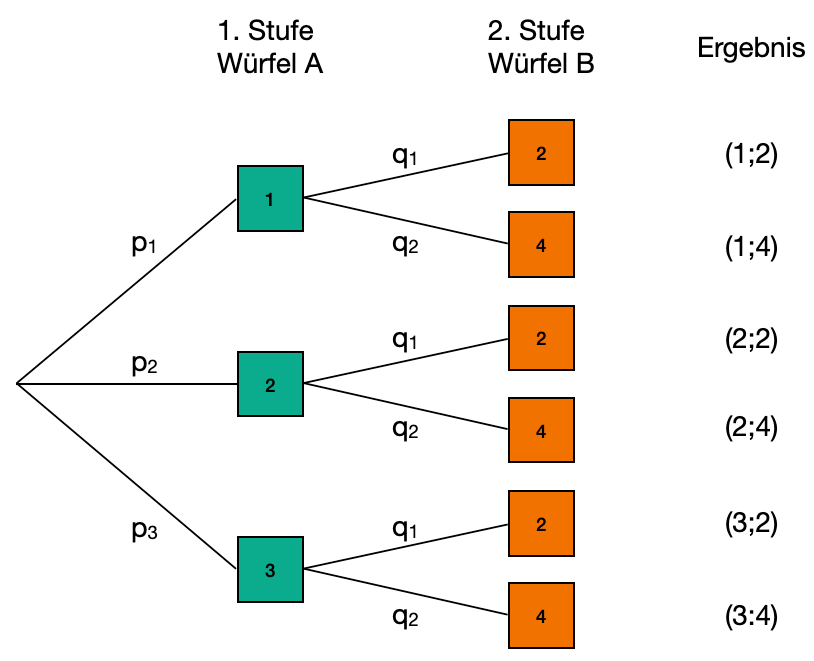
Bedingte Wahrscheinlichkeit
Wenn bei einem mehrstufigen Zufallsversuch ein Ereignis B bereits bekannt ist, so kann man das Ereignis in Abhängigkeit von B setzen. Man spricht dann von "durch B bedingte Wahrscheinlichkeit von A"
Es gilt:
Beispiel:
A: Augenzahl des Würfels ist gerade
B: Augenzahl des Würfels ist durch drei teilbar
| | ungerade | gerade |
| | 1 | 2 |
| | 5 | 4 |
| durch 3 teilbar | 3 | 6 |
Vierfeldertafel
Betrachtet man ein Zufallsexperiment mit den Stufen A und B, dann erhält man folgende Wahrscheinlichkeiten:
| | B | B ̅ | Summe |
| A | P(A und B) | P(A und B ̅ ) | P(A) |
| A ̅ | P(A ̅ und B) | P(A ̅ und B ̅ ) | P(A ̅ ) |
| Summe | P(B) | P(B ̅ ) | 1 |
| | B | B ̅ | Summe |
| A | | | |
| A ̅ | | | |
| Summe | | | |
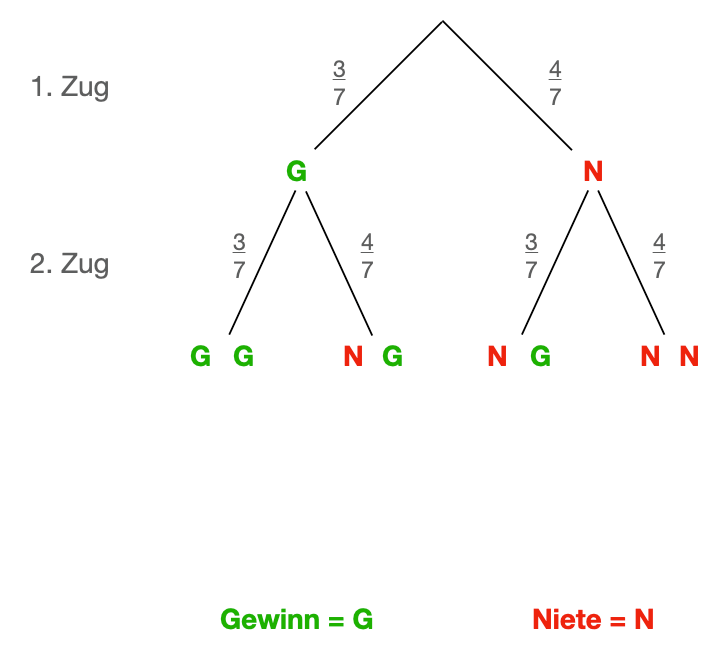
Ziehen mit Zurücklegen
In einem Behälter sind 7 Zettel (3 mal Gewinn und 4 mal Niete)
In diesem Beispiel wird nach dem Ziehen eines Zettels dieser vor dem zweiten Zug zurück gelegt. Es sind also immer 7 Zettel im Behälter.
Daraus ergibt sich folgendes Baumdiagramm
Ziehen ohne Zurücklegen
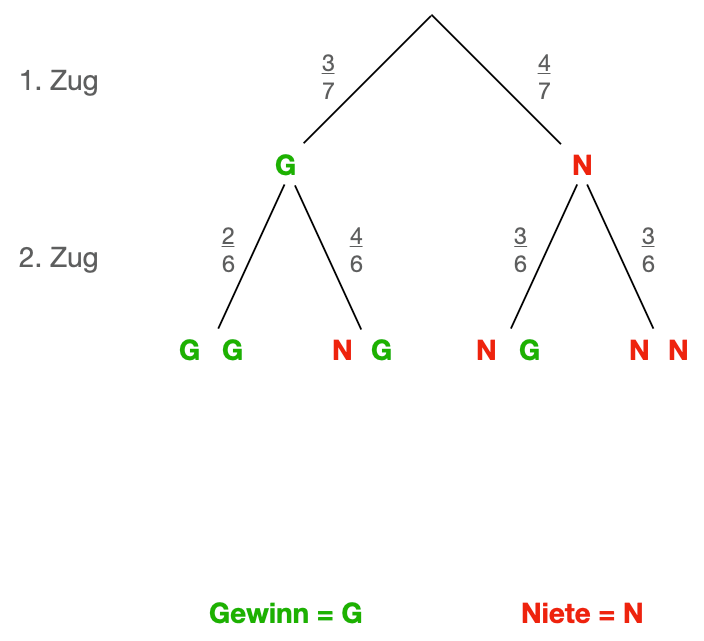
In einem Behälter sind 7 Zettel (3 mal Gewinn und 4 mal Niete)
In diesem Beispiel wird nach dem Ziehen eines Zettels dieser vor dem zweiten Zug nicht (!) zurück gelegt. Es sind also beim zweiten Zug nur noch 6 Zettel im Behälter.
Daraus ergibt sich folgendes Baumdiagramm
Drei Farben mit ziehen mit bzw. ohne Zurücklegen
Erwartungswert
Wenn man bei einem Zufallsversuch den einzelnen Ereignissen andere Größen zuordnet, dann kann man diese Zuordnungen mit zugehörigen Wahrscheinlichkeiten multiplizieren und aus deren Summe dann den so genannten Erwartungswert bilden.
Beispiel: Aus einem Behälter wird ein Zettel gezogen. Bei "Gewinn" erhält man 4€, bei "Niete" muss man 3€ bezahlen.
Wenn in dem Behälter nun 3 Zettel mit "Gewinn" und 4 Zettel mit "Niete" vorliegen (7 Zettel insgesamt) , dann erhält man folgenden Erwartungswert:
P(einen Gewinn oder eine Niete ziehen) = P(G,N) + P(N,G)