母は分解をgenerateする
1.母関数って何か
このワークシートはMath by Codeの一部です。
数や関数を並べた列、たいていは数列{An}に対して、
これを係数をする多項式、形式的なべき級数 ΣAnx^nやΣ(Anx^n/n!)を
{An}の母関数といいます。
nは有限でなくてもよく、このべき級数も収束するかは問わない形式的なべき級数です。
無限次元にしたとしても、無限の程度を問うわけでもなく、形式的に有界にしていないだけです。
規則性を見つけるための無限なので、使う部分はわりと低次元の項どうしの計算だったりします。
そもそも多項式は、整数と同じで、たし算、定数倍、積で閉じた集合体、環なので、
整数と同じように自由に+,×,k倍ができるね。
また、項別に微分をしたり、級数の和を求めるなどの式の変形ができたり、
いろんな視点とからめて数学分野を横断する技として使えます。
・例1
{An}={1 }のとき、an=[1,1,1,1,1,......]の母関数はf(x)=1+x+x2+x3+.......ですね。
これを等比数列の和の公式と極限を使って、f(x)=1/(1-x)とかけますね。
つまり、母関数f(x)は、1/(1-x)=1+x+x2+x3+...... のように、
まとめた式=バラした式の形にかけるね。
・例2
{An}={nCr | 0≦r≦n, nはn∈N の定数}のとき、an=[nC0, nC1,......,nCn-1,nCn}の母関数は
f(x)=(1+x)n=nC0x0+nC1x+....+nCn-1xn-1+nCnxnですね。
ここで母関数fにx=1を代入すると、2n=nC0+nC1+....+nCn-1+nCnが、
ここで母関数fにx=-1を代入すると、0=nC0-nC1+....+(-1)nnCnが得られます。
母関数のxに値を代入すると、バラした値=まとめた値ができるね。
・例3
母関数を微分する。例1の1/(1-x)=1+x+x2+x3+......は
左辺の微分=d((1-x)-1)/dx=-1(1-x)-2(1-x)'=1/(1-x)2
右辺の微分=0+1+2x+3x2+.....=Σkxk-1=Σkxk/x=1/xΣkxkだ。
これから、1/(1-x)2=1/xΣkxk。つまり、x/(1-x)2=Σkxkと言える。
右辺は{An}={n|n∈N},an=[1,2,3,4,....]の形式的なべき級数、つまり母関数といえる。
母関数を微分することで、別の母関数を作ることができたということだね。
・例4
母関数の指数を取り出す個数と考えて、かけ算してみよう。
(1+x+x2+x3+x4)(1+x+x2+x3)(1+x+x2)=1+3x+6x2+9x3+11x4+11x5+9x6+6x7+3x8+x9
3つの母関数は5円玉が4枚以下、10円玉が3枚以下、50円玉が2枚以下の取り出しとする。
3つの母関数の積の母関数は、係数は場合の数を、指数は取り出した合計個数をあらわします。
3x8は合計8枚の取り出しが3通りあることに対応する。
・例5
母関数をn回かけ算する。
例1の1/(1-x)=1+x+x2+x3+.....をn回かけると、
1/(1-x)n=(1+x+x2+x3+.....)(1+x+x2+x3+.....)(1+x+x2+x3+.....)........(1+x+x2+x3+.....)
右辺を展開したときのxkの係数は、n個のカッコから指数和がkになるように取り出す数、
たとえるとn個の箱から重複をゆるして合計k個とりだす数、
つまり、k個の物とn-1個のしきり物からk個選ぶ組み合わせ、つまり、n+k-1Ckとなるね。
1/(1-x)n=Σn+k-1Ckxkとなり、数列{n+k-1Ck}の母関数は(1+x+x2+x3+.....)n=1/(1-x)n
母関数をかけ算すると、別の母関数ができました。
・例6
母関数の指数をシフトしてn回かける。
例1の1/(1-x)=1+x+x2+x3+.....を両辺x倍すると、x/(1-x)=x+x2+x3+.....
となるね。これは、1個以上選ぶことを表してるね。
これをn回かけると、xn/(1-x)n=(x+x2+x3+.....)n=xn(x+x2+x3+.....)nとなる。
これと例5から、(x+x2+x3+.....)n=xnΣn+k-1Ckxk(k=0から∞)=Σr-1Cr-nxr(n+k=r=nから∞)
数列{r-1Cr-n}の母関数ができたね。
n+k=rの置き換えをしたので、rはn以上。
xrの係数は、n個から重複を許してr個取り出す数であり、それがr-1Cr-nになることがわかった。
・例7
合計金額と考えてかけ算すると、係数は種類をまぜた組み合わせを表す。
(1+x5+x10+x15+x20)(1+x10+x20)(1+x50+x100+x150)
=1+x5+2x10+........... + 2x160+2x165+3x170+2x175+2x180+x185+x190
3つの母関数の指数は5円玉4枚以下、10円2枚以下、hが50円3枚以下で作れる金額を表す。
積の母関数の係数が場合の数で、指数はまぜた合計金額になる。
3x170は合計金額が170円になるのが3通りあることを表しているね。
・例8
文字xにtxのように区別文字つきのxを代入して種類を特定できる。
例1の1/(1-x)=1+x+x2+x3+.....のxにtxを代入すると、1/(1-tx)=1+tx+t2x2+t3x3+.....
母関数の指数を取り出す個数と考えて、かけ算するときに区別文字を入れる。
(1+ax+a2x2+a3x3+a4x4)(1+bx+b2x2+b3x3)(1+cx+c2x2)の展開でx8は合計8枚の取り出し方になる。
係数はa3b3c2+a4b3c+a4b2c2これから、a,b,cから合計8枚選ぶ組み合わせは(3,3,2),(4,3,1),(4,2,2)。
2.数の分割と母関数
数の分割decompose,divide,partitionとは、
その数自身または、それ以外の数の和の組み合わせの式のことで、
分割数はその総数です。
たとば、3の分解は3,2+1,1+1+1があり、分割数は3(通り)です。
・例9
xにxpを代入すると、(xp)n=xnpから、
例1の母関数f(xp)は、1/(1-xp)=1+xp+x2p+.....xkp+
n個からp個単位で取り出すことを表します。このpを1,2,3,4,....として母関数をかけたものは
1/{(1-x1)(1-x2)(1-x3)(1-x4).....}=ΣxkΣx2kΣx3kΣx4kΣ..... = 1 + 1x+2x2+3x3+5x4+7x5+....
nの和分解decomposeの数はxnの係数に等しい。
(検証)母関数の係数を分離したリストを作る
1/(1-x1)=1+x1+x2+x3+x4+x5 -> [1,1,1,1,1,1]
1/(1-x2)=1+x2+x4 -> [1,0,1,0,1,0]
1/(1-x3)=1+x3 -> [1,0,0,1,0,0]
1/(1-x4)=1+x4 ->[1,0,0,0,1,0]
1/(1-x5)=1+x5 ->[1,0,0,0,0,1]
右辺の積は1+x1+2x2+3x3+5x4+7x5 +.......
x4の係数は5。これは、4の[4, 3+1, 2+2, 2+1+1, 1+1+1+1]の5通りの和分解に一致する。
x5の係数は7。これは、5の[5, 4+1, 3+2, 3+1+1,2+2+1,2+1+1+1,1+1+1+1+1]の7通りの和分解に一致する。
質問:例9の考え方を使って、整数Nの和分解をする関数を作るにはどうしたらようでしょうか。
多項式の係数を取り出します。つぎに逆順にして繰り上がらないx進法(xが巨大)として
係数をかけ算します。筆算でもできますよ。
[1,1,1,1,1,1] reverse-> 111111
[1,0,1,0,1,0] reverse-> 010101
[1,0,0,1,0,0] reverse-> 001001
[1,0,0,0,1,0] reverse-> 010001
[1,0,0,0,0,1] reverse-> 100001
10になっても繰り上がりせずに、111111×010101(mod 1000000) = 332211
332211×1001(mod 1000000)=543211
543211×10001(mod 1000000)=653211
653211×100001(mod 1000000)=753211となります。つまり、
111111*10101*1001*10001*100001 % 1000000= 753211
このreverseして、[1,1,2,3,5,7]になりますね。
これで、1から5まで和分解の数がわかる係数の数列ができました。
このような発想でnを和分解する関数decompo(n)を作ってみよう。
ポイントは、1からnまでのそれぞれの倍数を表す母関数リストgenefは静的に作れます。
だから、宣言型、関数型プログラミングが向いています。
次に母関数のかけ算ですが、逆転してからかけ算して、最後にもとに戻すのは
筆算には向いています。プログラミングでは、あえて逆転せずにそのままできます。
係数リストの番号が、母関数の次数を表していると考えれば、0次の定数項が0番、
1次の係数がリストの1番、、、、と考えると、n次の係数はリストのn番となるからです。
n個の関数1の倍数のgenef[0]からnの倍数のgenef[n-1]までを全部かけ算して、
xnの係数を求めよう。
このかけ算は、かけ算の結果、状態が変化するプロセスなので
動的な、通常の手続きのくり返し型のプログラミングが向いているでしょう。
[IN]Python=========================================================
def decompo(n):
max_id = n+1
genef = [] # 反復後の母関数係数のリスト
indexs = [x for x in range(max_id)]
for i in range(1,max_id):
genef.append(list(map(lambda x : 1 if x % i ==0 else 0, indexs)))
print(f"{n}の和分解をするために、母関数をかける。prev*current")
prev = genef[0]
# prevの初期値はgenefの先頭の母関数
for i in range(1,max_id-1):
ans = [0]*(3*n)
current = genef[i] #currentはgeneの1以上の母関数
print(f"prev = {prev},current = {current}")
for k in range(max_id): # current のk番を動かす
if current[k]==1:
for j in range(max_id): #prevをkけたシフトしてansに加算
ans[j + k] += prev[j]
for l in range(max_id):
prev[l] = ans[l] #ansの内容をprevに必要な分だけコピー
print(f"関数積 {prev}から、{n} の分解数={ans[n]}")
return True
decompo(4)
decompo(6)
decompo(9)
[OUT]=============================================
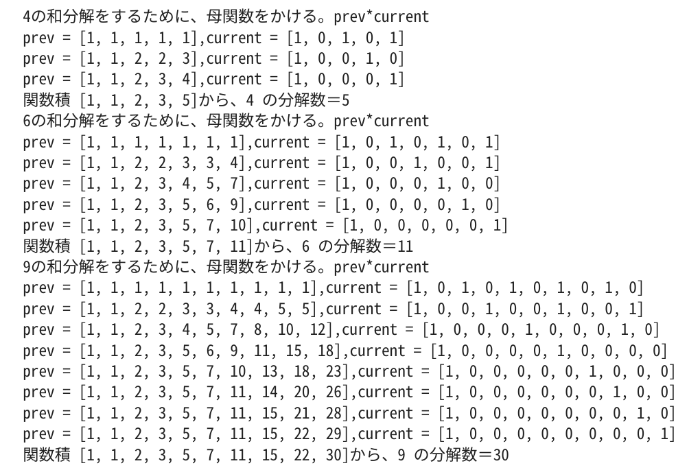
4の和分解をするために、母関数をかける。prev*current
prev = [1, 1, 1, 1, 1],current = [1, 0, 1, 0, 1]
prev = [1, 1, 2, 2, 3],current = [1, 0, 0, 1, 0]
prev = [1, 1, 2, 3, 4],current = [1, 0, 0, 0, 1]
関数積 [1, 1, 2, 3, 5]から、4 の分解数=5
6の和分解をするために、母関数をかける。prev*current
prev = [1, 1, 1, 1, 1, 1, 1],current = [1, 0, 1, 0, 1, 0, 1]
prev = [1, 1, 2, 2, 3, 3, 4],current = [1, 0, 0, 1, 0, 0, 1]
prev = [1, 1, 2, 3, 4, 5, 7],current = [1, 0, 0, 0, 1, 0, 0]
prev = [1, 1, 2, 3, 5, 6, 9],current = [1, 0, 0, 0, 0, 1, 0]
prev = [1, 1, 2, 3, 5, 7, 10],current = [1, 0, 0, 0, 0, 0, 1]
関数積 [1, 1, 2, 3, 5, 7, 11]から、6 の分解数=11
9の和分解をするために、母関数をかける。prev*current
prev = [1, 1, 1, 1, 1, 1, 1, 1, 1, 1],current = [1, 0, 1, 0, 1, 0, 1, 0, 1, 0]
prev = [1, 1, 2, 2, 3, 3, 4, 4, 5, 5],current = [1, 0, 0, 1, 0, 0, 1, 0, 0, 1]
prev = [1, 1, 2, 3, 4, 5, 7, 8, 10, 12],current = [1, 0, 0, 0, 1, 0, 0, 0, 1, 0]
prev = [1, 1, 2, 3, 5, 6, 9, 11, 15, 18],current = [1, 0, 0, 0, 0, 1, 0, 0, 0, 0]
prev = [1, 1, 2, 3, 5, 7, 10, 13, 18, 23],current = [1, 0, 0, 0, 0, 0, 1, 0, 0, 0]
prev = [1, 1, 2, 3, 5, 7, 11, 14, 20, 26],current = [1, 0, 0, 0, 0, 0, 0, 1, 0, 0]
prev = [1, 1, 2, 3, 5, 7, 11, 15, 21, 28],current = [1, 0, 0, 0, 0, 0, 0, 0, 1, 0]
prev = [1, 1, 2, 3, 5, 7, 11, 15, 22, 29],current = [1, 0, 0, 0, 0, 0, 0, 0, 0, 1]
関数積 [1, 1, 2, 3, 5, 7, 11, 15, 22, 30]から、9 の分解数=30
例10
6色の色紙がそれぞれ6枚ずつあるとする。これから重複を許して6枚選ぶ組み合わせを求める。
同じ母関数を6回かけよう。
(1+x1+x2+x3+x4+x5+x6)6 を展開して、x6の係数をもとめればよいね。
6=6, 5+1, 4+2, 4+1+1, 3+3, 3+2+1, 3+1+1+1, 2+2+2, 2+2+1+1, 2+1+1+1+1,1+1+1+1+1+1から多項定理から、
6C1+6*5+6*5+6*5C2+6!/(3!3!)+6P3+6*5C3+6!/(2!2!2!)+6C2*4C2+6C1*5C4+6C6
=6+30*2+60+20+120+60+15+90+30+1=462通りだね。
質問:例10の6種6枚から重複して6選ぶ重複組み合わせをコードで求めるにはどうしますか。
例9では母関数がnだけあったけれど、重複組み合わせでは、同じ1つの母関数をn乗するだけだから、
むしろ、しくみは簡単になるね。
母関数の係数であるgeneリストは定数項もあるので、1をn+1個並べたもの。
かならずかけ算になるので、ifは不要になるし、1倍だから、
シフトするだけというしくみも同じになるね。
#[IN]Python
def dblcombi(n):
max_id = n+1
gene = [1]*max_id
print(f"{n}の重複組み合わせを求めるために、母関数を{n}回かける。")
prev = gene
# prevの初期値はgenefの先頭の母関数
for i in range(1,max_id-1):
ans = [0]*(3*n)
print(f"prev^{i} = {prev}")
for k in range(max_id): #current のk番を動かす
for j in range(max_id): #prevをkけたシフトしてansに加算
ans[j + k] += prev[j]
for l in range(max_id):
prev[l] = ans[l] #ansの内容をprevに必要な分だけコピー
print(f"prev^{n} = {prev}から、{n}枚の組み合わせ数={ans[n]}")
return True
dblcombi(6)
dblcombi(8)
#=========================
[OUT]
6の重複組み合わせを求めるために、母関数を6回かける。
prev^1 = [1, 1, 1, 1, 1, 1, 1]
prev^2 = [1, 2, 3, 4, 5, 6, 7]
prev^3 = [1, 3, 6, 10, 15, 21, 28]
prev^4 = [1, 4, 10, 20, 35, 56, 84]
prev^5 = [1, 5, 15, 35, 70, 126, 210]
prev^6 = [1, 6, 21, 56, 126, 252, 462]から、6枚の組み合わせ数=462
8の重複組み合わせを求めるために、母関数を8回かける。
prev^1 = [1, 1, 1, 1, 1, 1, 1, 1, 1]
prev^2 = [1, 2, 3, 4, 5, 6, 7, 8, 9]
prev^3 = [1, 3, 6, 10, 15, 21, 28, 36, 45]
prev^4 = [1, 4, 10, 20, 35, 56, 84, 120, 165]
prev^5 = [1, 5, 15, 35, 70, 126, 210, 330, 495]
prev^6 = [1, 6, 21, 56, 126, 252, 462, 792, 1287]
prev^7 = [1, 7, 28, 84, 210, 462, 924, 1716, 3003]
prev^8 = [1, 8, 36, 120, 330, 792, 1716, 3432, 6435]から、8枚の組み合わせ数=6435
3.指数型の母関数
数列{An}の母関数は数列を係数にしてつくった。
それ以外に係数/n!にして作る方法もある。
この形式を使うと、収束するときの関数などでも便利に使えるようになる。
例2.1
{An}=[1,1,1,1,.....]で Σ xk/k!=1+x+x2/2!+ .....=ex
無限級数の和は、自然対数eを使った指数関数になる。
言い換えると、数列{1}の母関数が、exのマクローリン展開を与えていることになる。
そんなわけで、この形を指数型の母関数と呼ぶことが多い。
例2.2
例2.1をn回かけて展開すると、f(x)= (1+x/1+x2/2!+ .....)n=enx
この母関数の右辺は例2.1のxにnxを代入したと見ることができるね。
だから、f(x)=Σ(nx)k/k!=Σ(nk)xk/k!となる。だから、
これは{An}=nk、n通りがk回反復する数だから、n個から重複OKでk個選ぶ数
重複順列の母関数だとわかるね。
例2.3
例2.1の式を変形すると、x+x2/2!+ .....=ex−1。これをm回かけた式は(ex−1)m
一方で、2項定理の式から
(ex−1)m=((ex)+(-1))m=Σ (mCm-k(ex)m-k(-1)k)=Sum(mCk (-1)ke(m-k)x ,k,0,m)
また、例2.1のxに(m-k)xを代入すると、e(m-k)x=Sum((m-k)nxn/n!, n,0,∞)
これを上の式に代入して、(ex−1)m=Sum(mCk (-1)k (Sum( (m-k)nxn/n! ), n, 0, ∞), k, 0, m)
sumとsumの間のmCk (-1)k は、nの変化を受けないから定数扱いしてSumの中に入れられる。
その後、2重のΣはよこの合計をたてに合計しても、たての合計をよこに合計しても最後は同じなので、
Σの内、外を入れえよう。
=Sum(Sum ((-1)kmCk (m-k)n) , k, 0, m) xn/n!) , n, 0, ∞)
結局、
(ex−1)m=Σ (Σ((-1)kmCk (m-k)n)) xn/n!)
m!で両辺をわると、
(ex−1)m/m!=Σ (Σ((-1)kmCk (m-k)n)/m!) xn/n!) =Σ S2(n,k) xn/n!
第2種スターリング数の指数型の母関数が(ex−1)m/m!となったね。
例2.4
0個もありうるときはΣ xk/k!=1+x+x2/2!+ .....=ex
1個以上のときは、0乗の項がないので、x2/2!+ .....=ex−1
こう考えると、場合の問題に指数型母関数を使うこともできるね。
1から5までの数をr個並べるとき、1,2,3は1個以上並べ、4,5は0個以上並べるとしたら、
母関数の積は(ex−1)3(ex)2=(e3x−3e2x+3ex−1)(e2x)=e5x−3e4x+3e3x−e2x
=Σ (5x)k/k!+Σ (-3(4x)k/k!)+Σ( +3(3x)k/k!)+Σ(- (2x)k/k!) =Σ (5k-3*4k +3*3k- 2xk)xk/k!
Σの線形性からΣを分配法則のように1つにまとめることができるね。
だから、xrの係数5r-3*4r +3*3r- 2rが、求める場合の数になる。
r=5のときは5**5-3*4**5 +3*3**5- 2**5=750通りになるね。
例2.5
m人をA,B,Cの3部屋に空き部屋ができないように1人以上入れるとき振り分け方の数
A,B,Cの3つの記号をm個並べるのと同じだから、例2.4と同様にできる。
母関数の積は(ex−1)3=e3x−3e2x+3ex−1=Σ (3k-3*2k +3)xk/k! -1
だからxmの係数3m-3*2m +3が求める場合の数になる。
たとえばm=8のときは、3^8-3*2^8+3 = 5796通りになるね。
4.オイラーの分割
オイラーは2種類の分割が同数になることを、母関数が一致することで証明した。
2種類の分割とは、
数Nを異なる整数に和分解と数Nを奇数だけに和分解のことだ。
例4.1
・6を異なる整数に和分解する方法は4通り
6,5+1,4+2,3+2+1
・6を奇数だけに和分解する方法は4通り
5+1,3+3,3+1+1+1,1+1+1+1+1+1
例4.2
・9を異なる数に和分解する方法は8通り
9, 8+1,7+2,6+3,6+2+1,5+4,5+3+1,4+3+2
・9を奇数だけに和分解する方法は8通り
9, 7+1+1,5+3+1,5+1+1+1+1,3+3+3,3+3+1+1+1,3+1+1+1+1+1+1,1+1+1+1+1+1+1+1+1
オイラーは巧妙な方法で分割数が同一であることを一般的に証明しました。
nを異なる数に和分解する母関数Qは(1+xi)(iは1,2,3,.....)の積になります。
理由は、それぞれはnの分解に1,2,3,...を使うかどうかの選択を表しているので、同じ数を2回以上使うことはないからです。
6=3+3という分割ができませんが、6=3+2+1の分割はできますね。
Q=(1+x)(1+x2)(1+x3).......... = 1+x+x2+2x3+2x4+3x5+4x6+..........
証明のために、Qの符号をマイナスにした式
P=(1-x)(1-x2)(1-x3)..........を用意しよう。
PQ=(1+x)(1+x2)(1+x3)..........・(1-x)(1-x2)(1-x3).........
=(1+x)(1-x)(1+x2)(1-x2)(1+x3)(1-x3).........
=(1-x2)(1-x4)(1-x6)...............
PQ/P=(1-x2)(1-x4)(1-x6).........../(1-x)(1-x2)(1-x3).........
=1/(1-x)(1-x3)(1-x5).........
=Rとします。指数が偶数の項が約分して、奇数だけが残りました。
さてこれは何でしょう。
PQ/P=Qであることは明らかですが、
最後の式Rは例1や例9に出てきた、分数式を級数の和に直すと意味を思い出せるね。
1/(1-x)=1+x1+x2+x3+x4+.... (1をいくつか使う)
1/(1-x3)=1+x3+x6+x9+x12+....(3をいくつか使う)
1/(1-x5)=1+x5+x10+x15+x20+....(5をいくつか使う)
つまり、これらの積Rは奇数だけをいくつか使った和分解を表す母関数です。
だから、Q=Rとなるのです。
オイラーは、すばらしいですね。