Euklid am Schönen Brunnen - als Vertreter der Geometrie

Euklid verfasst um 300 v.Ch. das wohl bedeutenste Mathematikbuch der Welt: Die Elemente
Seine besondere Leistung besteht darin, die mathematischen Erkenntnisse anderer Gelehrter (u.a. Pythagoras) in hervorragender didaktischer Form (mit Postulaten, Axiomen und Definitionen) zusammengefasst zu haben.
Das 5. Postulat ist wohl das berühmteste: Das Parallelenpostulat
(Bemerkung: es ist deshalb so berühmt, weil man bis in die Neuzeit versucht hat, das Postulat zu beweisen und nicht glauben wollte, dass es ein Postulat ist.)
Das Parallelenpostulat im Wortlaut:
"Und daß, wenn eine gerade Linie beim Schnitt mit zwei geraden Linien bewirkt, daß innen auf derselben Seite entstehende Winkel zusammen kleiner als zwei Rechte werden, dann die zwei geraden Linien bei Verlängerung ins unendliche sich treffen auf der Seite, auf der die Winkel liegen, die zusammen kleiner als zwei Rechte sind."
![Bemerkung:
Insbesondere zum Beweis von Satz 29 (in den Elementen von Euklid) benötigt man das Parallelenpostulat:
Bei zwei gegebenen parallelen Geraden [u]müssen[/u] die Winkel ([math]\alpha[/math] und [math]\beta[/math]) zusammen das Maß 180° ergeben. D.h. das Parallelenpostulat dient dazu, die Eindeutigkeit von Parallelen darzustellen!](https://www.geogebra.org/resource/bewphaj3/ICIUqOIPTBrIaANK/material-bewphaj3.png)
Heute würde man das Parallelenpostulat vielleicht so formulieren:
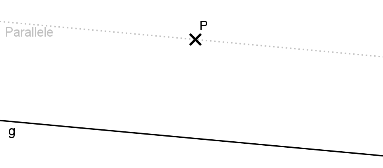
Prof. Albrecht Beutelspacher erklärt das Parallelenpostulat ganz wunderbar in der Folge Wie hat alles angefangen? in seiner Reihe Mathematik zum Anfassen (ab Minute 7).
Link zum Video