Parametrización de curvas
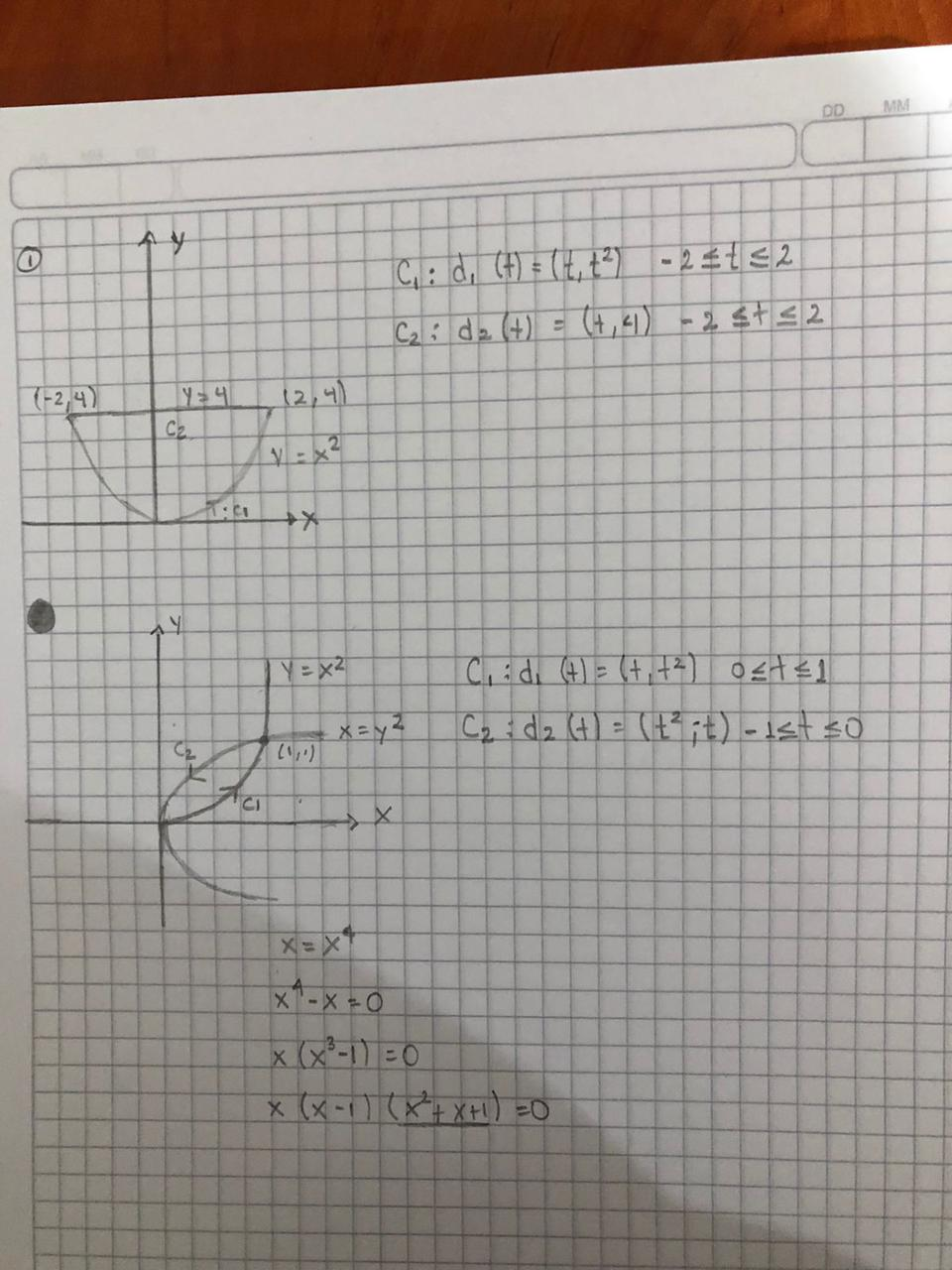
Consideramos una curva en el plano como una línea trazada sobre un papel, tal como puede ser una línea recta, una curva parabólica o una circunferencia. Este par de ecuaciones, que muchas veces es una forma conveniente para describir una curva, se llama ecuaciones paramétricas de la curva en el plano:
x = f(t)
y = g(t)
Cada valor de t determina un punto (x, y) en el plano. Cuando t varía (en un intervalo de números reales), el punto (x, y) = (f(t), g(t)) se mueve generando una curva en el plano.


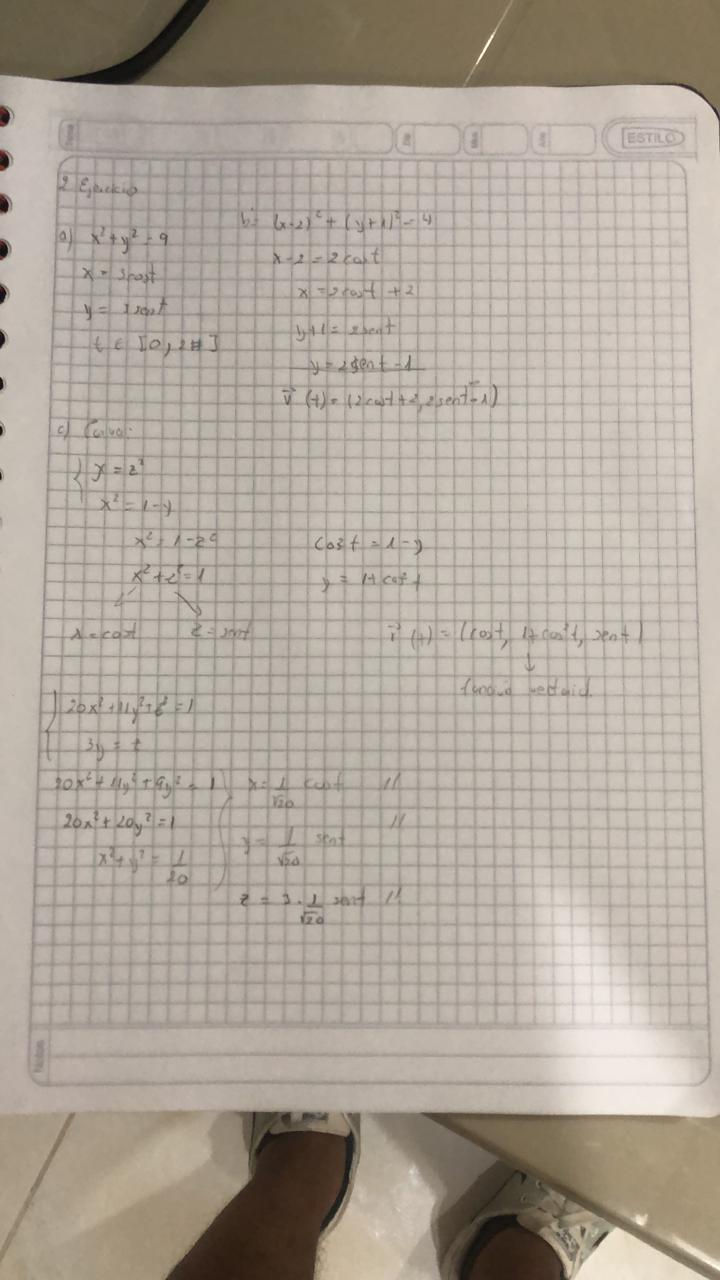
Funciones vectoriales de un parámetro
Una función con valores vectoriales es una función cuyo rango o imagen es un conjunto de vectores ~r (t), cuyo dominio está en la recta real (intervalo I, cerrado o semicerrado, o toda la recta) y cuyo rango o imagen está formado por vectores del espacio o del plano. Se tiene :~r: I ⊂ R → Vn donde n = 3 ´o 2 Una función vectorial de un parámetro representa una región del plano o del espacio que no es una región solida ni una superficie, sino que podríamos decir que es un “objeto unidimensional”: ~r(t) representa una curva paramétrica en el espacio o en el plano coordenado. Ejemplo El movimiento de una partícula en el plano está definido por la siguiente función vectorial: ~r1(t) = (4 cost, 4 sen t), 0 ≤ t≤ 2π Graficar la curva imaginaria que describe la partícula al moverse, indicando los puntos iniciales y final, así como el sentido del recorrido. b). Si el movimiento está representado por ~r2(t) = (−4 sen(2t), 4 cos(2t)), con 0≤ t ≤ 2π, ¿cuál es la curva determinada? a) Las funciones componentes son x1(t) = 4 cost e y1(t) = 4 sen t. Si para algunos valores de t situamos en el plano los puntos P(x1(t), y1(t)), o sea P (4 cost, 4 sen t), su ubicación parece indicarnos que la curva es una circunferencia (evalúe ~r1(t) en t = π 4 , π 2 , π, 3π 2 ). Si eliminamos el parámetro t entre las ecuaciones x = x1(t), y = y1(t), obtenemos la ecuación cartesiana de la curva. Para ello, en este caso conviene sumar las componentes al cuadrado para eliminar el parámetro, entonces queda: x 2 + y 2 = [x1(t)]2 + [y1(t)]2 = (4 cost) 2 + (4 sen t) 2 =16 cos2 t + 16 sen2 t = 16(cos2 t + sen2 t) = 16 luego x 2 + y 2 = 42 .