Relación entre la Distribución Binomial y la Normal.
1. Introducción.
Las distribuciones binomial y normal están muy relacionadas entre sí. En ocasiones realizar algunas actividades con la distribución binomial resulta muy difícil o laborioso. En esos casos la distribución normal con unos sencillos ajustes, puede resultarnos muy útil para los cálculos.
2. Actividad.
Una empresa de móviles sabe que está fabricando aproximadamente el 12 % de sus aparatos con algún defecto.
Una empresa distribuidora afirma que ha recibido 18 móviles en mal estado en una compra que ha hecho de 100. Contesta a las siguientes preuntas:
- Si llamamos x al número de móviles defectuosos que envía la fábrica ¿qué distribución de probabilidad se ajusta mejor al problema y por qué?
- Calcula la probabilidad de enviar 18 móviles en mal estado de 100.
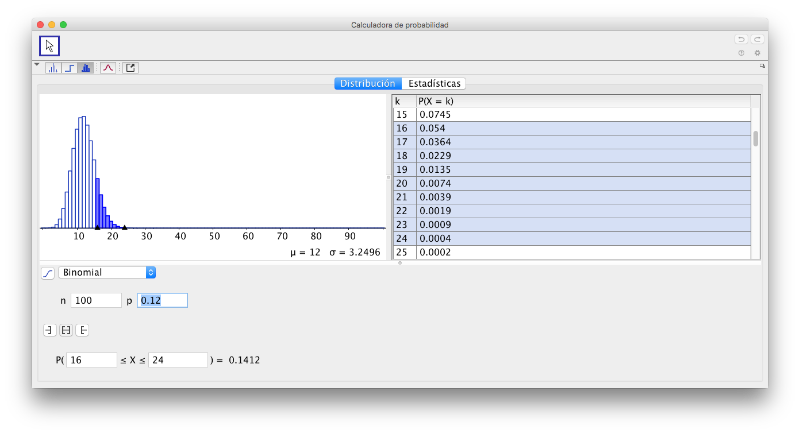
- La empresa distribuidora afirma que en todos los envíos de 100 móviles, le están llegando entre 16 y 24 móviles en mal estado. Calcula la probabilidad de que en un envío se manden entre 18 y 24 móviles defectuosos.
- ¿Se puede calcular el apartado 3 empleando una distribución normal? Si es así, explica el por qué e indica el tipo. Realiza los cálculos que consideres oportunos.
- ¿Se puede calcular el apartado 2 utilizando una distribución normal?
3. Resolución.
1. El ejercicio se ajusta a una distribución binomial, puesto que:
- Los sucesos son independientes entre sí. El que un móvil esté defectuoso no implica que el siguiente lo esté o no.
- El experimento se realiza muchas veces, en concreto 100.
- Hay dos probabilidades que son éxito sacar un móvil defectuoso y fracaso no sacarlo.
Cálculos de una binomial en GeoGebra.
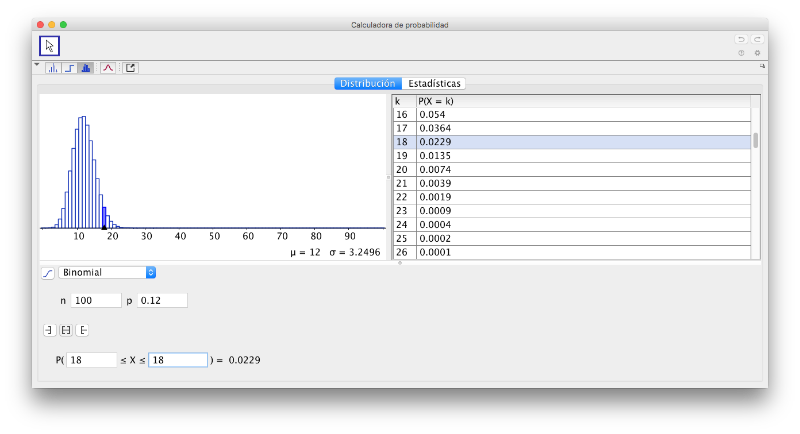
3. Para realizar este ejercicio con una binomial, tendríamos que hacer los siguientes cálculos:
Estos cálculos son bastante largos y complicados. Solo con ayuda de una buena calculadora se pueden realizar. En este caso GeoGebra es una magnífica herramienta que permite la resolución fácilmente:
4. Si nos fijamos en las gráficas de los apartados anteriores, la binomial se parece mucho a una campana de Gauss. Esto nos indica que entre las dos distribuciones de probabilidad, hay mucha relación.
La teoría matemática nos dice que si:
, y, , entonces la Binomial y la normal son muy aproximadas. En concreto, en este ejercicio:
De esto se deduce que
Podemos ver que son aproximadas en la siguiente construcción de GeoGebra.
Actividad de GeoGebra que relaciona la Distribución Binomial con la Normal.
En esta actividad de GeoGebra podemos modificar los valores y veremos como se calculan las probabilidades en la Binomial y la Normal y salen muy aproximadas. El problema es que las dos gráficas no ajustan igual.
La Binomial son rectángulos de base 1 y altura la probabilidad de ese valor.
La Normal es una curva llamada campana de Gauss y la probabilidad es el área entre los dos valores que nos piden. Ésto se hace mediante una operación matemática llamada integral definida.
Si nos fijamos entre la binomial y la normal quedan unos pequeños picos que se compensan con los huecos que hay dentro. Para ello, hay que utilizar un valor de 0,5 a los valores que nos interesan, unas veces sumados y otras restados, para que nos quedemos exactamente con los rectángulos de la binomial que nos interesan. Al final los números que se calculan mediante la binomial y los de la normal salen muy parecidos. Jugando con la gráfica de la actividad de GeoGebra se puede ver lo necesarios que son esos 0,5 que utilizamos.
En este apartado calculando tenemos que:
Si y , haciendo los cálculos necesarios obtenemos que:
Aunque los resultados no son iguales salen muy aproximados.
5. Aunque la distribución normal no calcula probabilidades para valores puntuales, puesto que esta probabilidad es 0 en variable continua (recordar que la probabilidad es el área debajo de una curva y para un valor concreto de x no puede haber área pues sería solo una línea), también podemos aplicar la normal al problema del apartado 2. En este caso jugaremos con ese 0'5 que restamos y añadimos al valor que nos pidan. En este caso el ercicio quedaría así:
El valor se aproxima muchísimo al resultado del apartado 2.
4. Conclusión.
Como vemos la distribución binomial y la normal se parecen mucho bajo unas determinadas circunstancias.
Ahora con la construcción de GeoGebra en pantalla, podemos hacer probaturas con otros tipos de distribuciones binomiales, ver las normales que se aproximan a ellas y realizar algunos ejercicios con la binomial, viendo si los resultados nos salen aproximados con la distribución normal.
Ahora bien, si dispones de una calculadora Casio fx-570 SPX ó 991 SPX, puedes resolver resolver estos problemas de una manera muy sencilla. Aquí dejo un vídeo que enseña a realizar este tipo de ejercicios con ayuda de la calculadora.