Householder Transformation ℝ³ A = QR
Alle Berechnungen/Vektoren basieren auf Listen/Matrizen, da auch höhere Dimensionen als R3 bedient werden sollen und das dyadische Produkt u uT zweier Vektoen (MHouseHolder()) damit darstellbar ist.
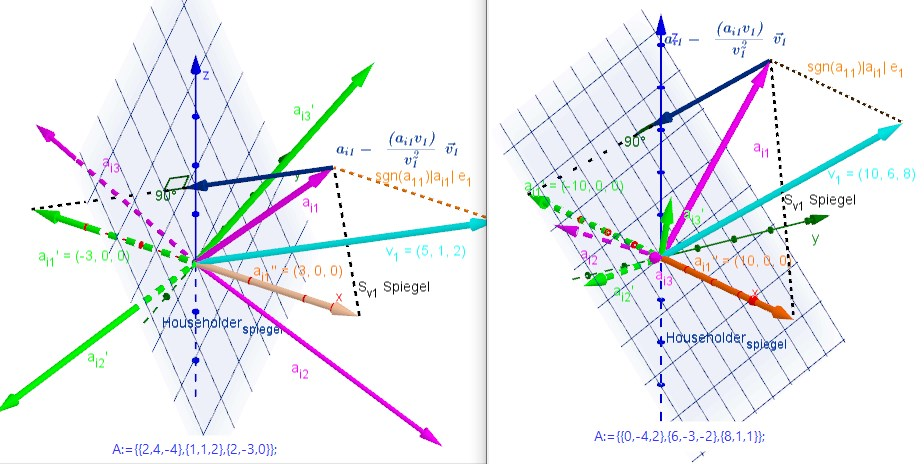
Veranschaulichung 1. Step
A = {ai1, ai2, ai3}
v1 Achse um ai1 auf die x-Achse zu spiegeln ai1'' , Householder-Spiegelung (berücksichtigt sgn(a11)):
v1 Normalenvektor der Householder Spiegelebene
H: v1 x=0
→ ai1 ∈ HHNF → Abstand HHNF(ai1) = d = ai1 v1 /√(v1²)
→ Lotfusspunkt [90°] = ai1 - d v1 /√(v1²) = ai1 - ai1 v1 /√(v1²) v1 /√(v1²) = ai1 - (ai1 v1)/v1² v1
→ Spiegel-Vektor ai1' = ai1 - 2 (ai1 v1)/v1² v1
→ Matrixgleichung durch Ausklammern: (idn - 2 (v1 v1T)/v1²) ai1 - Dyadisches Produkt v1 v1T
→ (idn - 2 (v1 v1T)/v1²) {ai1, ai2, ai3} =
A1 = {ai1',ai2',ai3'}
1. Spalte a1i1 → {a111, 0, 0}
2. Step
----
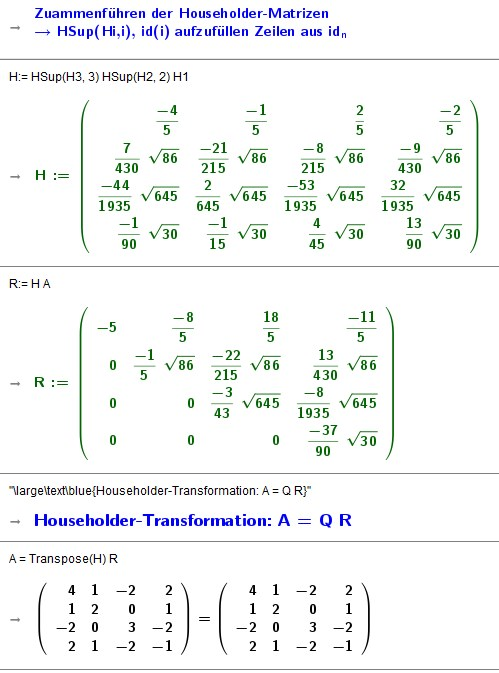
Erweitern der Householder Entwicklung über CAS-Functions
Spalte k von A: aik = Element(Transpose(A),k )
H:=HSup(H4, 4) HSup(H3, 3) HSup(H2, 2) H1
Aufgabe R4
----
Erweitern der Householder Entwicklung über CAS-Functions
Spalte k von A: aik = Element(Transpose(A),k )
H:=HSup(H4, 4) HSup(H3, 3) HSup(H2, 2) H1
Aufgabe R4
Beispiel R⁴
Übersicht bewahren - Rundung
