Log vs Exponents
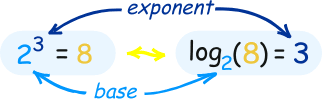
Reflection on the Application of Log and Exponents
Logarithmic functions are the inverses of exponential functions. The inverse of the exponential function y = ax is x = ay. The logarithmic function y = logax is defined to be equivalent to the exponential equation x = ay. y = logax only under the following conditions: x = ay, a > 0, and a≠1. It is called the logarithmic function with base a. Consider what the inverse of the exponential function means: x = ay. Given a number x and a base a, to what power y must a be raised to equal x?
This unknown exponent, y, equals logax. So you see a logarithm is nothing more than an exponent. By definition, alogax = x, for every real x > 0.Below are pictured graphs of the form y = logax when a > 1 and when 0 < a < 1. Notice that the domain consists only of the positive real numbers and that the function always increases as x increases.
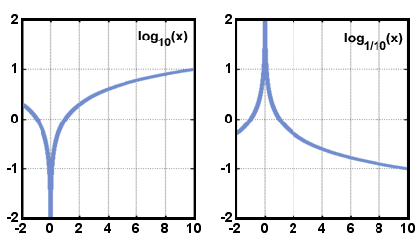Figure : Two graphs of y = logax. On the left, y = log10x, and on the right, y = log
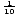x.The domain of a logarithmic function is real numbers greater than zero, and the range is real numbers. The graph of y = logax is symmetrical to the graph of y = ax with respect to the line y = x. This relationship is true for any function and its inverse.
Figure : Two graphs of y = logax. On the left, y = log10x, and on the right, y = log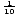x.The domain of a logarithmic function is real numbers greater than zero, and the range is real numbers. The graph of y = logax is symmetrical to the graph of y = ax with respect to the line y = x. This relationship is true for any function and its inverse.
Basic Rules to Remember
Here are the basic rules for exponents and logarithms:
**Exponent Rules:**
1. Product Rule: When you multiply two numbers with the same base, you can add their exponents.
am * an = a(m+n)
2. Quotient Rule: When you divide two numbers with the same base, you can subtract their exponents.
am / an = a(m-n)
3. Power Rule: When you raise a number with an exponent to another exponent, you can multiply the exponents.
(am)n = a(m*n)
4. Zero Exponent Rule: Any non-zero number raised to the power of zero is equal to 1.
a0 = 1 (where 'a' is non-zero)
5. Negative Exponent Rule: A non-zero number raised to a negative exponent is equal to the reciprocal of the number raised to the positive exponent.
a(-n) = 1 / an
6. Fractional Exponent Rule: A number raised to a fractional exponent is equivalent to taking the root of the number.
a(m/n) = n√(am)
**Logarithm Rules:**
1. Logarithm Definition: The logarithm of a number 'x' to the base 'b' (log_b(x)) is the exponent to which 'b' must be raised to obtain 'x'. In equation form:
logb(x) = y if and only if by = x
2. Logarithm of a Product: The logarithm of a product is equal to the sum of the logarithms of the individual factors.
logb(x * y) = logb(x) + logb(y)
3. Logarithm of a Quotient: The logarithm of a quotient is equal to the difference of the logarithms of the numerator and denominator.
logb(x / y) = logb(x) - logb(y)
4. Logarithm of a Power: The logarithm of a number raised to a power is equal to the exponent times the logarithm of the base.
logb(xy) = y * logb(x)
5. Change of Base Formula: If you need to find the logarithm of a number with a base different from the one available on your calculator, you can use the change of base formula:
- logb(x) = logc(x) / logc(b), where 'c' can be any positive base.
These rules are fundamental in solving exponential and logarithmic equations and manipulating expressions involving exponents and logarithms.