2. El método del barrido manual
Supongamos que tenemos dos puntos fijos A y B y queremos encontrar el lugar geométrico de los puntos que equidistan de ambos (la mediatriz) usando la propiedad Color Dinámico.
Colocamos un punto C libre e introducimos los valores a=Distancia[C,A], b=Distancia[C,B].
El lugar geométrico buscado estará formado por las posiciones del punto C para las cuales a=b.
Ahora buscamos expresiones algebraicas que tomen el valor 1 cuando a=b. Por ejemplo, a/b, b/a, 1+a-b, 1+abs(a-b), e^(-abs(a-b)), etc.
Colocamos cualquiera de esas expresiones (puede haber hasta 3 diferentes, una para cada valor R, G, B) como propiedad de Color Dinámico del punto C.
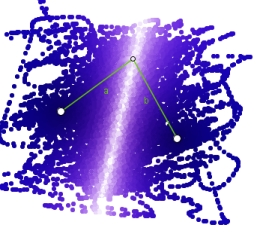
Supongamos, por ejemplo, que asignamos al punto C el color dinámico RGB=[a/b, a/b, a/b]. Al mover el punto C, con la traza activada, el rastro que deja va “pintando” la pantalla. Cuando se cumpla la condición a=b el valor RGB será [1,1,1], es decir, blanco:
Además de la mediatriz buscada, aparecen unas circunferencias no concéntricas rodeando al punto B. Cada circunferencia reúne a los puntos C que cumplen que "a es un múltiplo impar de b".
Esto es debido, como hemos visto, a la periodicidad del Color Dinámico. Si queremos eliminar esos otros lugares geométricos, basta reasignar el valor:
Si deseamos la aparición de colores, basta asignar diferentes expresiones algebraicas a cada R, G, B. Por ejemplo:
Además de la mediatriz buscada, aparecen unas circunferencias no concéntricas rodeando al punto B. Cada circunferencia reúne a los puntos C que cumplen que "a es un múltiplo impar de b".
Esto es debido, como hemos visto, a la periodicidad del Color Dinámico. Si queremos eliminar esos otros lugares geométricos, basta reasignar el valor:
RGB = [e^(-abs(a-b)), e^(-abs(a-b)), e^(-abs(a-b))]
Probamos a mover C por toda la pantalla y observamos el resultado:
Si deseamos la aparición de colores, basta asignar diferentes expresiones algebraicas a cada R, G, B. Por ejemplo:
RGB = [e^(-abs(a-b)), e^(-2 abs(a-b)), e^(-abs(a-b)/(a+b))]
Obsérvese que cuando "a" sea igual a "b" el valor numérico RGB continuará siendo [1, 1, 1], es decir, blanco: