cilinder, bol en kegel
Het artikel Archimedes en het volume van de bol (Pythagoras - 1 nov 2018) beschrijft hoe Archimedes de volumes van bol en kegel berekent t.o.v. het volume van een cilinder. Dit was gebruikelijk: de Grieken gebruikten geen aparte formules voor inhouden, maar drukten de volumes uit in verhoudingen.
De auteur van het artikel schrijft in moderne taal en vervangt de Griekse letters door Latijnse.
Net zoals in zijn berekening van een cilindersegment gebruikt Archimedes een balans.
Volg stapsgewijs de illustratie van de afleiding in het applet en de onderstaande tekst.
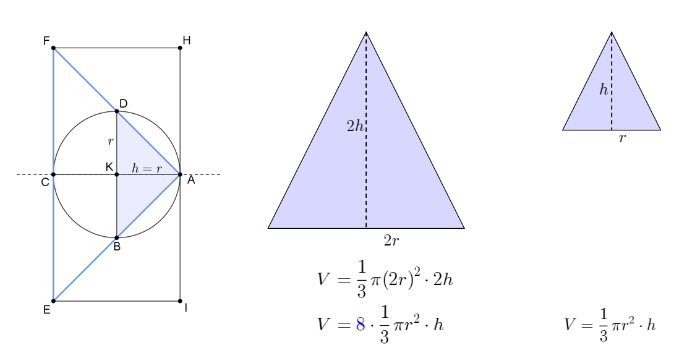
- Links zie je het zijaanzicht van de bol ABCD, de kegel AEF en de cilinder EFHI. Met de aanvinkvakjes toon je de lichamen in kleur. Rechts verschijnen ze in het draaibaar 3D-venster.
- Snij de lichamen door een versleepbaar vlak loodrecht op de as AC van de cilinder en bepaal de cirkelvormige doorsnedes met de drie lichamen.
- Verplaats de doorsnedes van kegel en bol naar een punt J op de as AC, waarbij |AJ| = |AC|. (Opmerking: Het is nu handig om de volumes te verbergen en enkel de doorsnedes te tonen) Archimedes creëert een balans met steunpunt A. - Links plaats hij de doorsnede met de cilinder en laststarm |AS|. - Rechts plaats hij de doorsnedes met de kegel en de cilinder en laststarm |AJ|. - Hij stelt vast dat voor elke doorsnede de balans in evenwicht is.
- Berekening van de oppervlaktes van de cirkels en de afstanden tot A bevestigen deze aanname.
Dit laat Archimedes vermoeden: “De oppervlakte van de bol moet gelijk zijn aan vier keer de oppervlakte van het grondvlak van deze kleine kegel ABD. Ik heb immers de intuïtie dat, aangezien elke cirkel gelijk is aan de driehoek met als basis de omtrek van de cirkel en als hoogte de straal, elke bol ook gelijk moet zijn aan de kegel met als grondvlak de oppervlakte van de bol en als hoogte de straal.”
Het is nu erg interessant om deze (moderne) tekst te vergelijken met de letterlijke vertaling die Jan Hogendijk maakte op basis van eerdere transcripties van de brief die Archimedes stuurt naar Eratosthenes.
In deze brief vermeldt Archimedes de reeds eerder bewezen verhouding tussen kegel en cilinder, zodat hij dit niet moet overdoen in zijn afleiding van het volume van een bol.
"Van Archimedes aan Eratosthenes, (ik hoop dat) het (je) goed gaat. Ik had je vroeger (enkele) van de (door mij) gevonden stellingen gestuurd, waarvan ik de beweringen had opgeschreven en gevraagd had de bewijzen te vinden, die ik op dat moment niet vermeld had...
... Op de volgende manier kan met dezelfde methode worden ingezien dat elke bol (gelijk) is (aan) vier maal de kegel met basis gelijk aan de grootste cirkel in de bol en hoogte gelijk aan de straal van de bol, en dat de cylinder met basis gelijk aan de grootste cirkel van de bol en hoogte de middellijn van de bol, anderhalf maal de bol is..."
(lees nu vooral verder via de hoger gegeven link en vergelijk beide manieren om wiskunde te beschrijven.)
standbeeld van Archimedes
Een van de inscripties op het standbeeld van Archimedes in Syracuse is een cilinder met een ingeschreven bol, verwijzend naar de afleiding van het volume van een bol.
