Lekcija 1.
Pretpostavimo da se dva podudarna kruga nalaze u paralelnim ravnima i da je svaki od njih ortogonalna projekcija onog drugog na odgovarajuću ravan. Površ koju obrazuju projektujući zraci tačaka datih kružnica naziva se cilindrična površ.
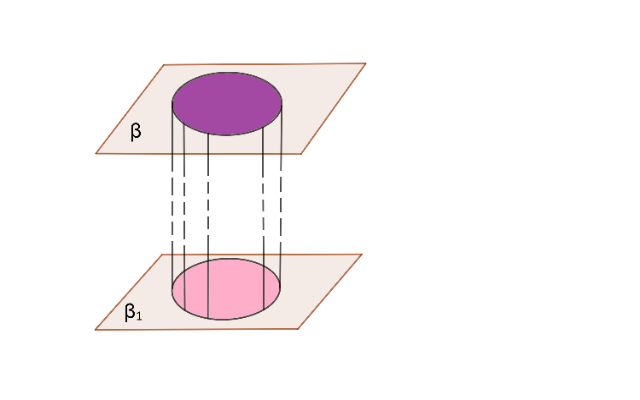
Geometrijsko telo ograničeno ovim krugovima i delom cilindrične površi između njih naziva se prav valjak.
Kako ćemo se baviti isključivo pravim valjcima, reč "prav" ćemo izostavljati.
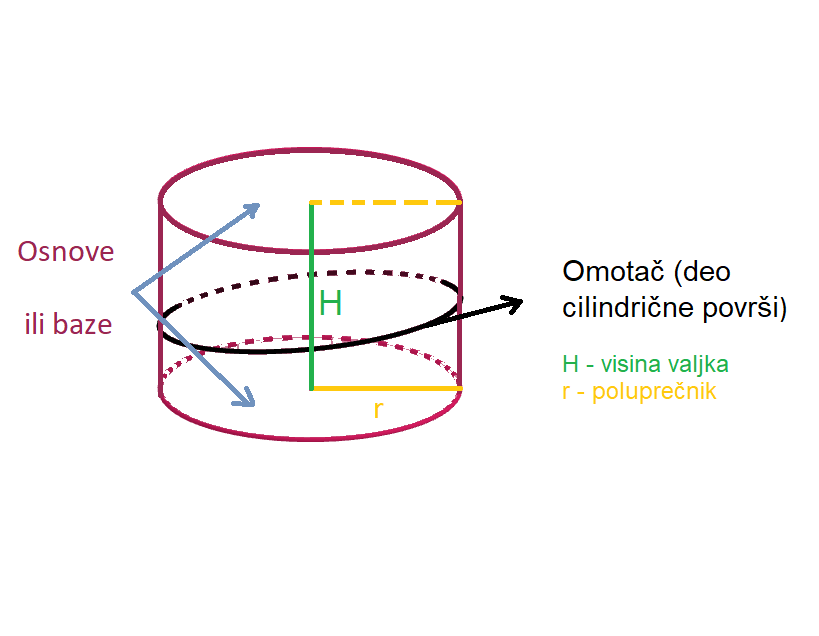
Krugovi su osnove ili baze valjka.
Deo cilindrične površi između ravni osnova naziva se omotač valjka.
Rastojanje između ravni osnova naziva se visina valjka.
Valjak je primer geometrijskog tela koje nije poliedar. On spada u takozvana obla tela.
Takođe, rotacijom pravougaonika oko jedne njegove stranice nastaje valjak. Preciznije, sve tačke prostora kroz koje prolaze tačke pravougaonika koji rotira obrazuju valjak.
Zbog toga se i kaže da je valjak rotaciono telo.
Rotacija pravougaonika i nastajanje valjka (kod n pomeranjem klizača vidi se proces rotacije, takodje, ako se u delu kod e umesto xOs stavi yOs, menja se osa rotacije).
Prava koja sadrži centre osnova valjka se naziva osa valjka.
Presek valjka i ravni koja sadrži osu valjka naziva se osni presek valjka.
Svi osni preseci valjka su međusobno podudarni.