Una función del plano en el plano...

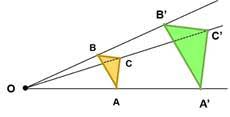
En el siguiente applet se muestra un triángulo ABC en el plano cartesiano. Multiplica cada una de las coordenadas del triángulo ABC por 2, anótalas y representa los puntos correspondientes en la cuadrícula y traza un nuevo triángulo (puedes llamarlo de triángulo DEF, siendo siendo D el correspondiente de A, el punto E el correspondiente de B, etc.) Repite el procedimiento, de forma tal de obtener al triángulo GHI, multiplicando las coordenadas del triángulo ABC por 3. Luego, utilizando las herramientas disponibles, responde:

1. ¿Qué relación existe entre las medidas de los lados del triángulo original con las de los triángulos DEF y GHI?
2. ¿Qué puedes afirmar acerca de los ángulos de los tres triángulos?
3. ¿Los triángulos DEF y GHI se corresponden al triángulo ABC a través de una isometría? ¿Por qué?

En la parte anterior hemos observado que los nuevos triángulos no se corresponden al ABC a través de una isometría ya que no se conservan las distancias. Ahora, en el siguiente applet podrás verificar las conjeturas anteriores utilizando el deslizador.

1. ¿Qué relación existe entre el valor que toma el deslizador y las coordenadas del nuevo triángulo (piensa en la forma que obtuvimos los nuevos triángulos en la parte anterior)?
2. Por otra parte deberás trazar las rectas que pasa por un punto y su correspondiente, es decir, deberás trazar las rectas (AA'), (BB') y (CC'). ¿Qué observas?

En esta actividad, trabajarás con un applet muy parecido al anterior, pero, en este caso el deslizador tomará otros valores.

1. ¿Es cierto que si asume un valor negativo la figura obtenida se reduce de tamaño?
2. ¿Para qué valores de se obtiene una figura de la "misma forma y tamaño"?
3. ¿Para qué valores de la figura "conserva su forma pero se reduce en tamaño"?
4. ¿Para qué valores de la figura "conserva su forma pero se amplia en tamaño
5. ¿Para qué valor de no obtenemos ninguna figura nueva?
6. Sintetiza tus respuestas anteriores considerando los valores de y utilizando el concepto de valor absoluto.