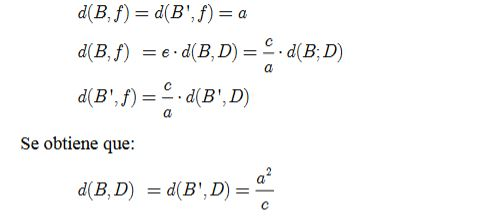Las cónicas como lugares geométricos.
Si consideramos el plano afín euclídeo, dado un punto f (denominado FOCO), una recta D (denominada DIRECTRIZ) y un número real e (denominado EXCENTRICIDAD). Denominamos CÓNICA C al conjunto de puntos del plano A cuya distancia al foco es igual al producto de e por su distancia a la directriz. Es decir:
Teniendo en cuenta que hay varios tipos de cónicas, según el valor de su excentricidad, podemos clasificar:
si e < 1 es una ELIPSE .
si e = 1 es una PARÁBOLA.
si e > 1 es una HIPÉRBOLA.
Como resumen, en el caso de las ecuaciones reducidas de las cónicas, los correspondientes focos, directrices y excentricidades vienen dadas por:

Como ejemplo de cónicas, estudiaremos los casos particulares de la parábola, la elipse y la hipérbola en sus formas canónicas (tomando un sistema de referencia adecuado).
ELIPSE
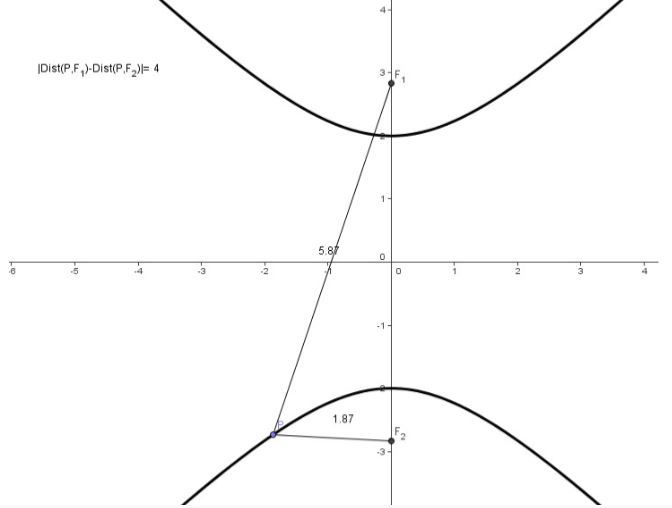
En el plano afín real E, se llama ELIPSE a la CÓNICA que tiene por focos los puntos f(C) y f‘(C’) (situados a una distancia dist(f,f’) = 2.c), y cuya constante es 2a ∈ R (siendo a>c), al lugar geométrico de los puntos P(x,y) de E, tales que:
dist(P,f) + dist(P,f’) = 2 a
Se denominan EJES de la elipse (por ser sus ejes de simetría ortogonales), a la recta que pasa por f y f’ (de segmento mayor) y a su mediatriz (de segmento menor)
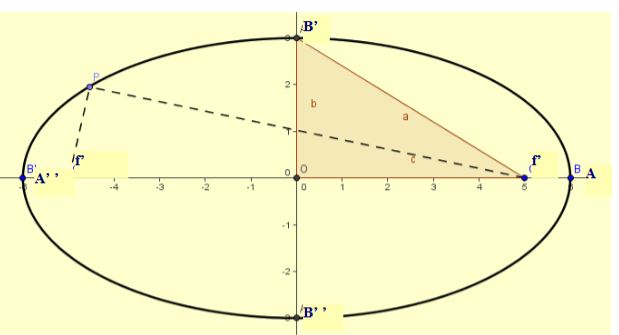
El punto de intersección de los ejes de la elipse, es su CENTRO, y los puntos de intersección con la elipse se denomina vértices (A y A‘ para el eje mayor, B y B’ para el eje menor).
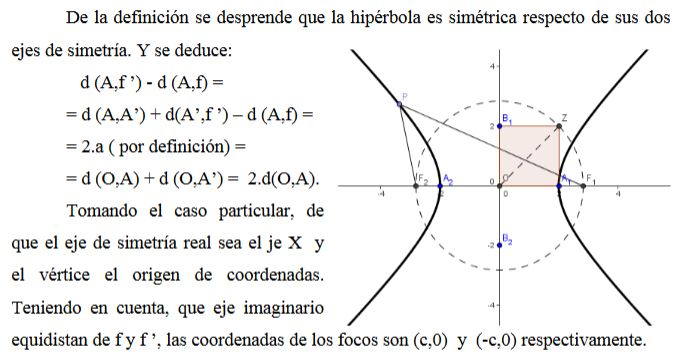
De la definición se desprende que la ELIPSE es simétrica respecto de los segmentos AA’ y BB’. De donde se deduce:
dist(A,f) + dist(A,f ’) = dist(A’,f) + dist(A’,f ’) = 2.a ( por definición ) =
= dist(O,A) + dist(O,A’) = 2. dist(O,A)
⇒ dist(O,A) = dist(O,A’) = a.
Y como los puntos B y B’, son simétricas respecto de los focos f y f’:
dist(B,f) = dist(B,f ’) = dist(B’,f) = dist(B’,f ’) = a
Denominando:
dist(O,B) = dist(O,B ’) = b.
Y teniendo en cuenta que
dist(O,f) = dist(O,f’) = c.
será:
Entonces, tomando el caso particular, de que los ejes mayores y menores de la elipse sean respectivamente el eje X e Y, de un sistema de referencia cartesiano.
Los focos f y f ’ tendrán de coordenadas (c,0) y (-c,0) respectivamente. Y para cada punto P de la elipse, la condición:
d (P,f) + d (P,f ’) = 2.a.



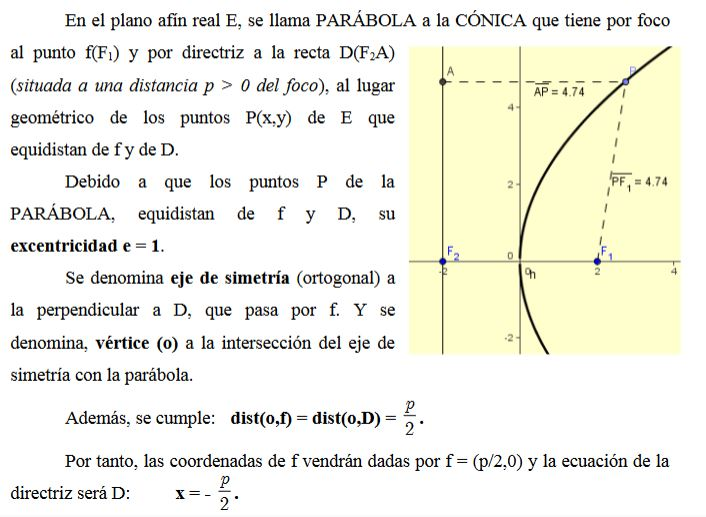
PARÁBOLA



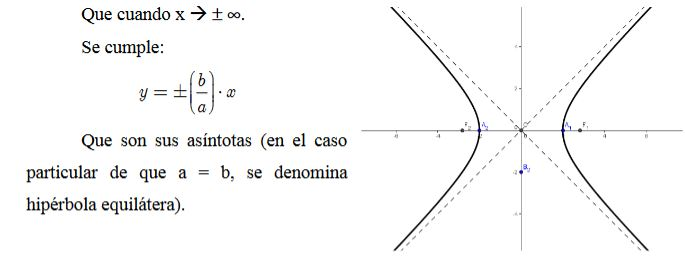
HIPÉRBOLA