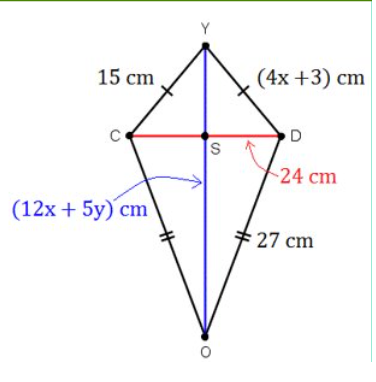
Kite Investigation
The figure below will always remain a kite regardless of how you move the vertices.
1. Click "Show all 4 angle measures." Move the vertices around. Write a conjecture about the angles in a kite.
2. Click "show diagonals." Then click "show additional angle measures." Write a conjecture about the diagonals of a kite.
The polygon above is called a kite. Is a kite a rhombus? Explain.
Is a kite a parallelogram? Explain.
Move the sliders on Kite above. Write 4 characteristics that you observe regarding the diagonals, angles and sides of the kite.
Are OPPOSITE SIDES of a kite congruent? If so, how many pairs?
Are ADJACENT SIDES of a kite congruent? If so, how many pairs?
Are any pairs of opposite angles of a kite congruent? If so, how many pairs?
Are the diagonals of a kite congruent?
What properties do a kite and a rhombus share (have in common)?
Search it.
What is the formula for the area of a kite?
Find the value of y given that the area of a kite is 552 square centimeters.