Les droites et les angles - Prise en main de Géogebra
Objectifs d'apprentissages
Dans cette activité, tu vas en apprendre un peu plus sur :
- Les droites : distinguer droites, demi-droites et segments (et comment les construire dans Geogebra)
- La position des droites : parallèles, sécantes et perpendiculaires (et comment les construire dans Geogebra)
- Les angles : types d'angles et comment les construire dans Geogebra
- Des droites remarquables : la bissectrice et la médiatrice
Les droites
D'abord, écoute les vidéos suivants sur les droites.
Les droites, demi-droites et les segments
La position des droites : parallèles, sécantes et perpendiculaires
Tracer des droites et des segments perpendiculaires et parallèles dans Geogebra
Dans l'appliquette ci-dessous, trace :
- Une demi-droite et une droite perpendiculaires;
- Deux segments parallèles.
À ton tour !
Observe les trois points M, N et P ci-contre et ensuite répond à la question ci-bas.

Combien de droites peuvent passer par les points suivants ?
a) M b) M et N c) M, N et P
Les angles
Écoute maintenant ces capsules sur les angles
Les types d'angles
Tracer un angle dans Geogebra
Dans l'appliquette ci-dessous, construis :
- Un angle obtu ;
- Un angle droit.
À ton tour !
Observe l'illustration suivante et réponds à la question ci-bas.
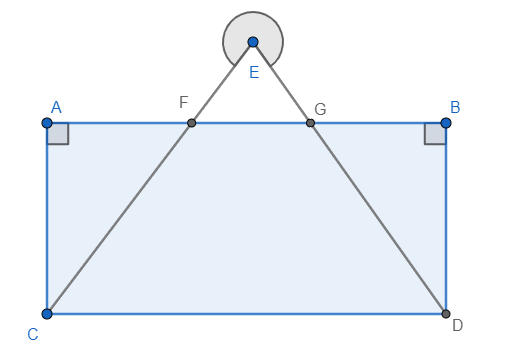
Trouve les angles demandés et nomme-les correctement
a) Un angle aigu b) Un angle obtu c) Un angle droit d) Un angle plat e) Un angle rentrant
Deux droites remarquables : la bissectrice et la médiatrice
Écoute ces capsules sur les droites remarquables
N.B. : isométrique signifie de même mesure
La bissectrice et la médiatrice
Tracer une bissectrice ou une médiatrice dans Géogebra
Réutilise ce que tu as appris dans la dernière vidéo pour construire dans l'appliquette les droites remarquables suivantes :
- La médiatrice du segment BC
- La bissectrice de l'angle A