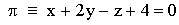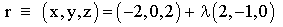8. Distancia de un punto a un plano/entre una recta y un plano/distancia entre dos planos
Distancia de un punto a un plano
La distancia de un punto, P, a un plano, π, es la menor de la distancia desde el punto a los infinitos puntos del plano. Esta distancia corresponde a la perpendicular trazada desde el punto al plano.
Si el punto está incluido en el plano la distancia es 0
Si el punto no está en el plano la distancia se determina de la siguiente forma:
![[math]u=QP[/math][math]P_0\left(x_0,y_0,z_0\right)[/math][math]\pi:Ax+By+Cz+D=0[/math][math]v=\left(A,B,C\right)[/math]](https://www.geogebra.org/resource/p9jcvdvk/yQHG8dsV1GvdlYDT/material-p9jcvdvk.png)
Demostración
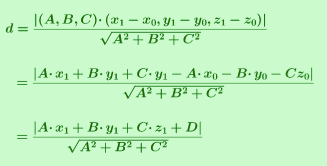
Ejemplo
¿Cuál es la distancia entre P(3,-1,2) y el plano π: 2x+y-z+1=0?
Solución
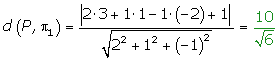
Distancia entre una recta y un plano
La distancia de una recta, r, a un plano, π, es la menor de la distancia desde la recta a los infinitos puntos del plano.
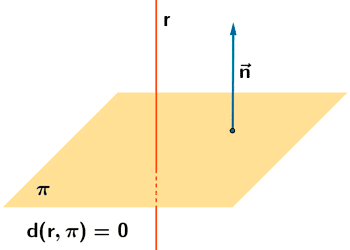
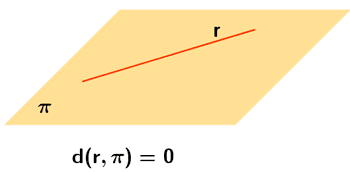
Si la recta está dentro del plano o son secantes la distancia es 0
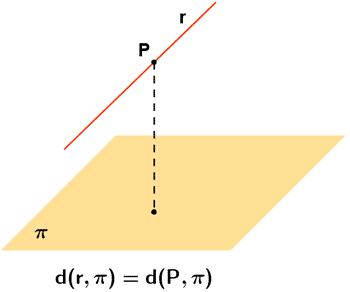
Si la recta y el plano son paralelos se toma un punto P y se calcula la distancia entre el punto P y el plano π
Ejemplo
Hallar la distancia entre la recta r, y el plano π
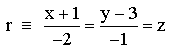
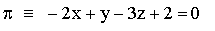
Solución
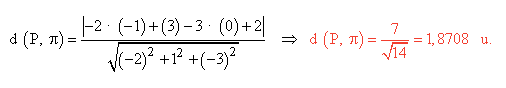
Distancia entre dos planos
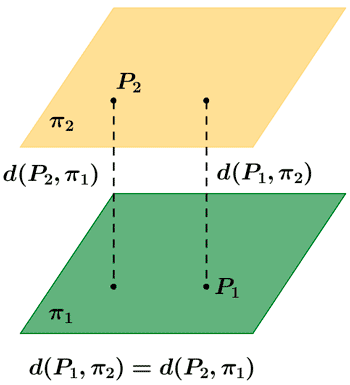
La distancia entre dos planos π y π' igualmente depende de su posición:
Si son planos coincidentes o secantes la distancia es 0
Si son planos paralelos la distancia entre ellos se calcula tomando un punto cualquiera en ellos y calculando la distancia de ese punto al otro plano, también se puede calcular de esta forma
Sea
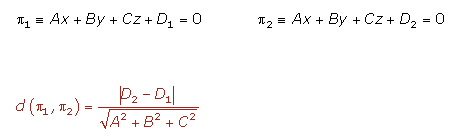
Ejemplo
Calcular la distancia entre lo planos π y π'
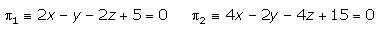
Solución
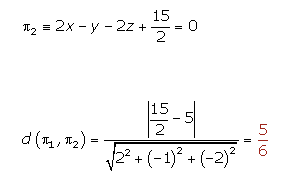
Preguntaaaa
¿Cuántas distancias puedes calcular desde un plano?
Ejercicios
1. Calcula la distancia entre el punto P(3,1,-2) y el plano π: 2y-3=0
2. Calcula la distancia entre el plano π y la recta r