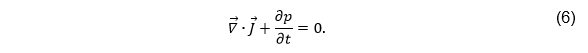Equações de Maxwell
As leis do eletromagnetismo clássico foram descobertas/elaboradas de modo fragmentado por Franklin, Coulomb, Gauss, Lorentz, Ampère, Faraday e outros. Mas, a unificação entre a eletricidade e o magnetismo foi finalizada por Maxwell ao incluir a corrente de deslocamento na lei de Ampère e formular o eletromagnetismo compactamente em 12 equações, as quais com a notação vetorial de Gibbs são as famosas quatro equações de Maxwell:

A equação (1) deve-se a Gauss. Dela se compreende que o campo elétrico tem como fonte ou sorvedouro a carga elétrica. A (2) implica na não existência de monopolos magnéticos, isto é, não há uma fonte ou sorvedouro. A (3) deve-se a Faraday, a qual afirma que a variação de campo magnético gera campo elétrico. E por fim, a (4) deve-se a Ampère, sendo o último termo adicionado por Maxwell. A qual diz que o campo magnético é gerado tanto por uma densidade de corrente elétrica como pela variação do campo elétrico no tempo.
Ademais, há também a expressão de força devida a Coulomb e Lorentz pertinente para a teoria. E, evidentemente, essas quatro equações oferecem muito mais que esse breve resumo. A exemplo, ao aplicar a identidade vetorial
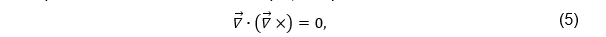
na equação (4), tendo ciência da (1), obtém-se a equação da continuidade, da qual infere-se a conservação da carga elétrica na natureza: