Obecná ortografická projekce
Obecná ortografická projekce je pravoúhlý průmět kulové plochy do její tečné roviny π, která není k zemské ose ani kolmá a ani s ní není rovnoběžná. Pokud bychom vedli středem kulové plochy rovinu ρ rovnoběžnou s rovinou π, pak průnik kulové plochy s rovinou ρ je obrysová kružnice, která není ani poledníkem a ani rovnoběžkou. Její průmět do roviny π je obrysem mapy. Dále již budeme zobrazovat pouze polokouli, která je popsána hraniční kružnicí, kterou jsme zmiňovali a bodem, kterým je bod dotyku kulové plochy s rovinou π.
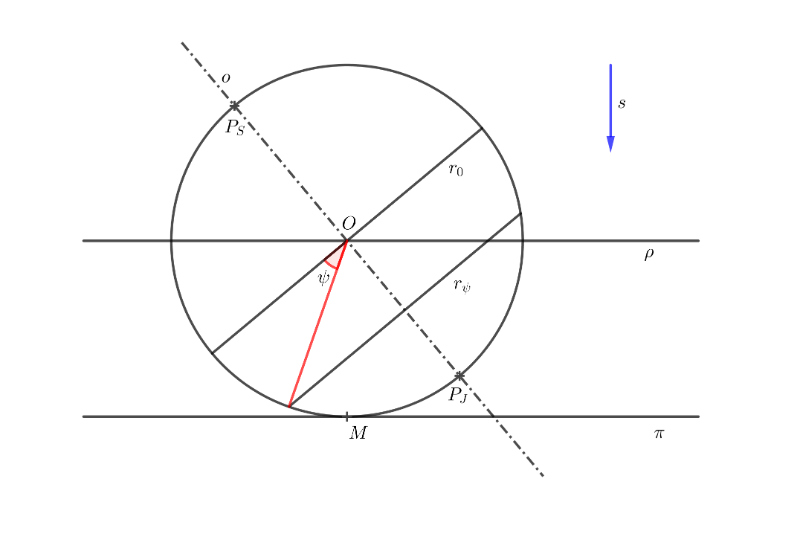
Obecnou ortografickou projekci tedy můžeme považovat za zobrazení kulové plochy v pravoúhlé axonometrii, která je svým středem umístěna do počátku soustavy souřadnic a jejíž rovník leží v rovině xy.
Konstrukce průmětů rovnoběžek
Průměty rovnoběžek konstruujeme pomocí sklopené promítací roviny, která je dána oběma póly a směrem promítání.
Konstrukce průmětů poledníků
Průměty poledníků jsou elipsy a opět je konstruujeme pomocí stejné sklopené roviny, jako u konstrukce rovnoběžek. V obou případech využíváme toho znalostí průmětu geografické sítě v rovníkové ortogonální projekci.