Kümelerin tanımı
Kümelerin tanımı
Küme nedir?
Alman matematikçi Georg (Corc Cantor) 1878 yılında yayımladığı makalesinde kümeyi, “iyi tanımlanmış birbirinden farklı nesneler topluluğu” şeklinde tanımlanmıştır. Bu tanımda bahsedilen “iyi tanımlama” ifadesi ortak özellikleri ile verilen bir kümedeki nesnelerin herkes tarafından aynı şekilde anlaşılması, anlamına gelir.
Küme, matematiksel anlamda tanımsız bir kavramdır. Bu kavram "nesneler topluluğu veya yığını" olarak yorumlanmaktadır. Bu tanımdaki "nesne" soyut ya da somut bir şeydir. Fakat her ne olursa olsun iyi tanımlanmış olan bir şeyi, bir eşyayı ifade etmektedir.
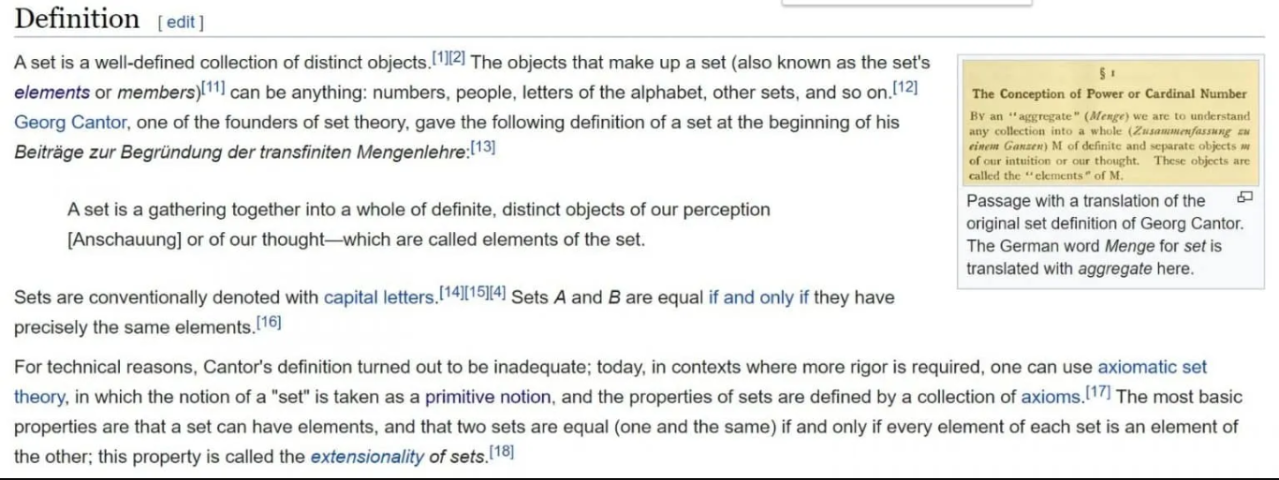
Ancak, kümenin tanımsız bir terim olduğunu söyleyen son paragraf atlanmış. Son paragrafın çevirisi şöyle:
“Teknik nedenlerden dolayı, Cantor’un küme tanımının uygun olmadığı ortaya çıkmıştır; günümüzde tutarlılığın önemli olduğu durumlarda, aksiyomatik küme kuramı kullanılabilir. Bu kuramda küme kavramı tanımsız terim kabul edilmektedir. (…)”
Burada, kümenin tanımsız bir terim olduğuna dair hiçbir bilgi verilmemiş. Cantor’un tanımı da küme tanımı olarak kabul edilmiş.
Yani kısaca, küme kavramı tanımsız kabul edilmiştir.
O halde kümenin bir tanımı var mı?
Sorun, modern matematiğin kurucularından olan Gottlob Frege ve Bertrand Russell arasındaki bir yazışmayla başlıyor. Frege, 20 yıl üzerinde çalıştığı ve matematiği mantığa indirgeyen kitabını yayınladıktan kısa bir süre sonra Russell’dan şu mektubu alır:
“Sayın Bayım, bugüne değin sizinki kadar titiz bir eserle karşılaşmamıştım. Her söylediğinize katılıyorum. Ancak bir konu kafamı çok kurcalamakta ve kendi başıma işin içinden çıkamadım. Kümelerin kendi kendini içerebileceğini söylemişsiniz. Kendi kendini içermeyen tüm kümelerin kümesi, kendi kendini içerir mi? İşte bu soruya bir yanıt bulamadım.”
Frege bu mektubu aldığında tüm kuramının çöktüğünü anlar, üzüntüden hastanelik olur. Russell, bu paradoksu Cantor’un çalışmalarını incelerken keşfetmiştir. Cantor’un “iyi tanımlanmış her nesneler topluluğu bir kümedir” tanımı, paradoksa yol açmaktadır.
Birçok küme kendisinin elemanı değildir. Örneğin, doğal sayılar kümesi, doğal sayı olmadığı için kendisinin elemanı değildir. Ama kendisinin elemanı olan kümeler de vardır. Örneğin domates olmayan tüm nesnelerin kümesi domates olmadığı için kendisinin elemanıdır.
Günümüzde, Frege’nin birçok fikrine yer veren Zermelo-Fraenkel Küme Kuramı’nın aksiyomları kullanılmaktadır. Bu kuram paradoksu ortadan kaldırmaktadır, ancak kuram içinde küme kavramı tanımsız bırakılmıştır.
Georg Cantor
Georg_Cantor
