Satz von Menelaos
1. Erarbeitung des Satzes
Gegeben seien Figuren, wie in Abbildung 1 dargestellt.
Auftrag 1
Beschreibe die in der Abbildung 1 dargestellten Figuren und die Lage zueinander.
Abb. 1: Dreieck und Gerade, die das Dreieck schneidet
Um herauszufinden, welche Zusammenhänge beim Satz von Menelaos in einem Dreieck wie aus Abb. 1 gelten, nutzen wir im folgenden die Abbildung 2. Durch Ziehen am Punkt E kann die Gerade so verschoben werden, dass sich die Lage der Schnittpunkte , und verändert. Dadurch entstehen verschiedene Längen der Teilstrecken (bspw. ).
Abb. 2: Dreieck mit angezeigten Längen der Teilstrecken
Auftrag 2
Übertrage die Tabelle 1 in dein Heft. Ermittle mindestens drei verschiedene Lagen der Gerade , sodass du jeweils drei unterschiedliche Längen für die Teilstrecken eintragen kannst.
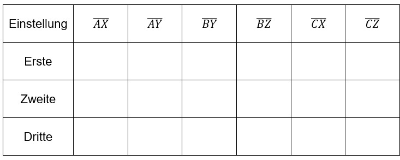
Tabelle 1: Übersicht über die Länge der Teilstrecken und den unterschiedlichen Einstellungen für die Lage der Gerade
Auftrag 3
Berechne nun, wie in Tabelle 2 vorgegeben ist, verschiedene Verhältnisse der Teilstrecken. Übertrage dazu die Tabelle in dein Heft und ergänze sie entsprechend deiner Größen aus Auftrag 1.
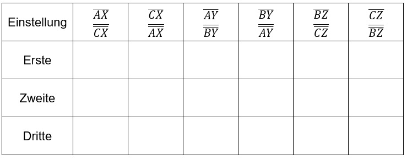
Tabelle 2: Übersicht über Verhältnisse der Teilstrecken
Auftrag 4
Berechne nun Produkte aus drei Faktoren. Verwende dazu ausschließlich Streckenverhältnisse aus der Tabelle 2 aus der ersten Zeile.
Beispiel:
Nicht erlaubt sind Kombinationen aus Faktoren, die zu einander den Kehrwert bilden. Bsp.:
Auftrag 5
Überprüfe für welche Kombinationen aus Auftrag 4, du das Produkt rund 1 erhältst.
Teste anhand der Einstellungen zwei und drei (also Zeile 2 und 3 der Tabelle 2) ob deine Vermutung auch hier zum Ergebnis rund 1 führt.
Auftrag 6
Formuliere mit eigenen Worten unter Verwendung deiner Erkenntnis aus Auftrag 5 den Satz von Menelaos.
Formulierungshilfe:
Wenn ein Dreieck ABC gegeben ist, welches von einer Geraden ..., dann gilt für die Teilstreckenverhältisse....