Uniform Convergent

Avtor:Selma Bayton

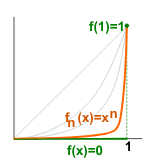
Uniform Convergence Explained

Sequence of functions

,

, 2, 3, ... is said to be uniformly convergent to

for a set

of values of

if, for each

, an integer

can be found such that

for

and all

.A series

converges uniformly on

if the sequence

of partial sums defined by

converges uniformly on

.To test for uniform convergence, use Abel's uniform convergence test or the Weierstrass M-test. If individual terms

of a uniformly converging series are continuous, then the following conditions are satisfied.1. The series sum

is continuous.2. The series may be integrated term by term

For example, a power series

is uniformly convergent on any closed and bounded subset inside its circle of convergence.3. The situation is more complicated for differentiation since uniform convergence of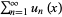

does not tell anything about convergence of

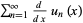. Suppose that

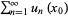converges for some

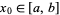, that each

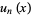is differentiable on

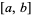, and that

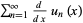converges uniformly on

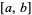. Then

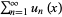converges uniformly on

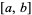to a function

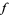, and for each

,

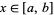Novi prispevki

Raziskovanje virov

Poglavja za raziskovanje