初速度为零的匀变速直线运动推论
若匀加速直线运动的初速度，加速度为，它的图像是过原点的直线，数学上是一个正比例函数。
这种运动相较于一般的匀变速直线运动有一些特殊的结论。
一、等时间间隔下的速度、位移推论
我们将匀加速直线运动按等时间间隔T（T为任意大小）切割为n份，有以下推论：
1、速度推论
时刻的速度,即速度与时间成正比，故我们有，
2、位移推论1
物体运动前秒的位移，位移与时间的平方成正比，即，
3、位移推论2
物体运动第秒的位移，则，
二、等位移间隔下的速度、时间推论
我们将匀加速直线运动按等位移间隔（为任意大小）切割为n份，有以下推论：
1、速度推论
位移和速度满足：，即。则，
2、时间推论1
物体运动位移和运动时间之间满足：，即，则，
3、时间推论2
物体在每段的运动时间,我们结合上一个规律即可得，
三、规律的应用情景
1、基本应用
若已知物体是从静止开始做匀加速直线运动，以上的规律可以直接应用。
例1：物体做初速度为零的匀加速直线运动，第一个2s、第二个2s和前6s内的位移之比为（ ）
解析：
取时间间隔T=2s，则第一个2s、第二个2s、第三个2s的位移比满足：,前6s的位移为，故D答案正确。
| A．1：3：5 | B．2：6：5 | C．2：8：7 | D．1：3：9 |
例2:（多选）如图所示，光滑斜面上的四段距离相等，质点从O点由静止开始下滑，做匀加速直线运动，先后通过a、b、c、d，下列说法正确的是（ ）
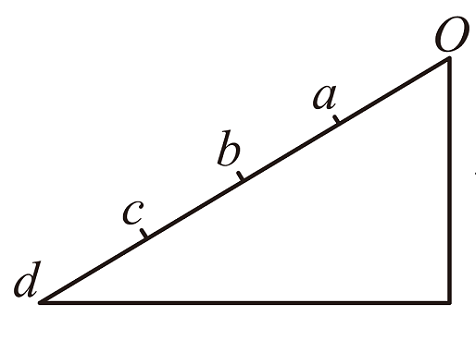
解析：
直接运用等位移比例可知B、C、D正确。b位置为整段运动的中间位置，中间位置速度不等于平均速度，A错。
A．质点在斜面上运动的平均速度 |
B．质点通过各点时的速率之比 |
C．质点依次通过各段距离的时间之比为 |
D．质点由O到达各点的时间之比 |
2、逆向思维应用
对于广义的刹车类问题，即物体从某个初速度减速为，我们可以用逆向思维把刹车看成倒放的从零加速运动，把这些比例式倒过来用即可。
例1：(多选)滑块以某一初速度从斜面底端O上滑到最高点D，用频闪仪记录的上滑过程如图所示，则（ ）
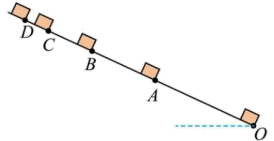
解析：
用逆向思维倒过来看，这个物体是从D静止释放的匀加速直线运动，满足等时间规律，速度比为，A正确；每段的位移比为：，D正确。
故选A、D。
| A．滑块在B点的速度大小为在C点的两倍 |
| B．滑块在A点的速度大小为在C点的两倍 |
| C．AB和CD的距离之比为3∶1 |
| D．AB和CD的距离之比为5∶1 |
例2：（多选）如图所示，用极薄的塑料膜片制成三个完全相同的水球紧挨在一起水平排列，子弹可视为在水球中沿水平方向做匀变速直线运动，恰好能穿出第三个水球，则可以判定(忽略薄塑料膜片对子弹的作用)( )
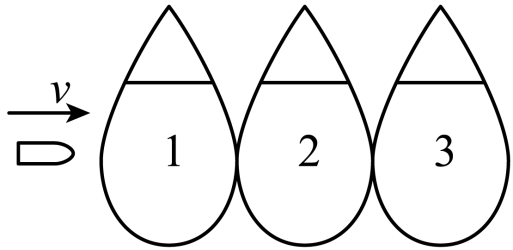
解析：
我们可以将子弹的运动看成是从3反向静止加速至1，由等位移规律，子弹在每个水球中的时间比为：，B对A错。传入每个水球的速度比为，D对C错。
故选B、D。
| A．子弹在每个水球中运动的时间之比 |
| B．子弹在每个水球中运动的时间之比 |
| C．子弹在穿入每个水球时的速度之比 |
| D．子弹在穿入每个水球时的速度之比 |
3、逆用规律判断物体运动时间和位置
等时间间隔内，做初速度为零匀变速直线运动物体的每段位移之比满足1：3：5：7……反过来说，若初速度为零做匀加速直线运动的物体每段位移比满足1：3：5……，则每段位移所用的时间T相等。
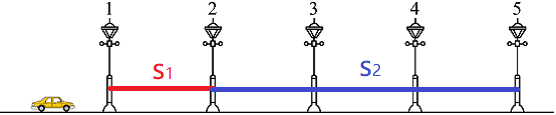
例1：如图所示，1~5是某平直道路上间距均为25m的路灯，轿车从第1个路灯由静止开始启动，经过20s正好到达第5个路灯。若将轿车视为质点，轿车做匀加速直线运动，则轿车过第2个路灯时的速度大小是（ ）
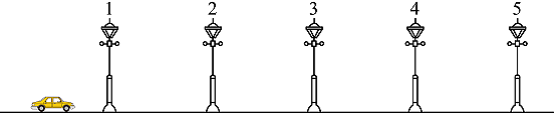
解析：
第1个路灯和第2个路灯的距离与第2个路灯和第5个路灯的距离之比为1：3，则汽车通过和通过所用的时间相同，通过第二个路灯的时刻恰为整段运动的中间时刻，，故选A。
A． | B． | C． | D． |
初速度为零的匀变速直线运动符合以上比例式，反过来说，符合这些比例式的匀变速直线运动初速度为0，不符合则初速度不为0。利用比例式我们可以判断物体初始点的位置。
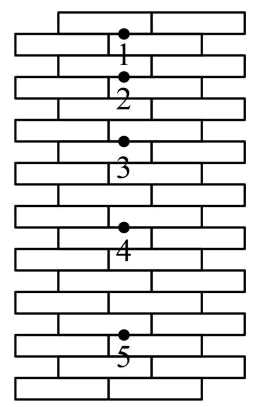
例2：小球从竖直砖墙某位置由静止释放，用频闪照相机在同一底片上多次曝光，得到了图中1、2、3、4、5所示的位置。已知连续两次曝光的时间间隔均为T，每块砖的厚度均为d，试判断1点是否为释放点。
解析：
从图中可以看出每相邻两段的位移差都成立，可以判断物体是做匀变速直线运动。但是各段位移之比为，不满足，可见1点并不是释放点。
解析：
从图中可以看出每相邻两段的位移差都成立，可以判断物体是做匀变速直线运动。但是各段位移之比为，不满足，可见1点并不是释放点。若释放点不知道，我们可以结合其他规律求解。
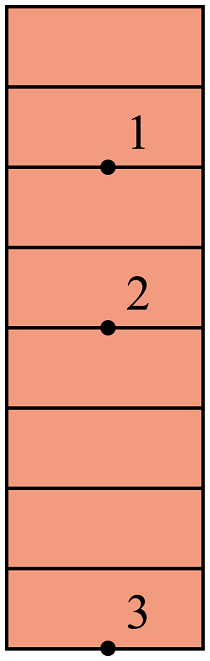
例3：某同学研究匀变速直线运动时，用一架照相机对正在下落的小球（可视为质点）进行拍摄，小球在空中的照片如图所示，1、2、3分别为连续相等时间间隔拍摄到的影像，每块砖的厚度均为d，且不计砖块之间的间隙，小球从静止开始下落，下落过程为匀加速直线运动。则小球开始下落点距影像2的距离为（ ）
解析：
，不满足，1点不是释放点。
设拍摄时间间隔为。两段位移差.
得 ①
2为1、3的中间时刻，由中间时刻速度等于平均速度推论： ②
释放点的速度为0，则释放点到2的距离满足：，
代入①、②解得：。
选A。
| A．2.55d | B．2.45d | C．2.35d | D．2.25d |